SSSUP: Sfera conduttrice con carica puntiforme interna
-
ilfugiuliopascal
- Messaggi: 14
- Iscritto il: 27 ago 2012, 11:46
SSSUP: Sfera conduttrice con carica puntiforme interna
Una sfera conduttrice cava che ha raggio interno R1 e raggio esterno R2 è caricata con una carica elettrica Q=3 nC. Una carica puntiforme q = 2 nC si trova nel vuoto al centro della sfera.
a) si calcolino le cariche elettriche Q1 e Q2 che si dispongono all'equilibrio sulle due superfici della sfera cava.
b) si trovi la forza totale esercitata dalla carica puntiforme sul conduttore
c) si dica che la posizione della carica puntiforme al centro della sfera è una posizione di equilibrio e, in caso affermativo, si dica se è equilibrio stabile, instabile o indifferente. Le risposte ad entrambi questi quesiti devono essere adeguatamente giustificate
a) si calcolino le cariche elettriche Q1 e Q2 che si dispongono all'equilibrio sulle due superfici della sfera cava.
b) si trovi la forza totale esercitata dalla carica puntiforme sul conduttore
c) si dica che la posizione della carica puntiforme al centro della sfera è una posizione di equilibrio e, in caso affermativo, si dica se è equilibrio stabile, instabile o indifferente. Le risposte ad entrambi questi quesiti devono essere adeguatamente giustificate
-
Roberto Albesiano
- Messaggi: 8
- Iscritto il: 8 mag 2012, 17:27
Re: SSSUP: Sfera conduttrice con carica puntiforme interna
Cerchiamo di capire la situazione:
1) hai una carica Q sulla superficie della sfera conduttrice, se non ci fosse nient'altro questa carica si disporrebbe sulla superficie esterna del conduttore
2) c'è una carica q nel centro della sfera, questa carica produce un campo elettrico centrale che sposta le cariche che sono sulla sfera su un'altra posizione di equilibrio. Ciò vuol dire due cose:
i. la carica totale sulla sfera è sempre Q
ii. il campo elettrico nel conduttore è, ovviamente, zero (altrimenti non sarebbe in equilibrio)
Quindi per il punto (a) devi imporre le condizioni


Dove con indico il campo elettrico tra
indico il campo elettrico tra 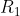 e
e 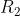 , che è la somma del campo prodotto dalla carica q (
, che è la somma del campo prodotto dalla carica q ( * q/r^3 * \vec r) )
)
e quello prodotto dalle cariche sulla superficie (che puoi trovare con il teorema di Gauss, considerando una sfera di raggio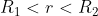 )
)
Per (b) puoi osservare che per simmetria la forza totale è nulla, mentre per (c) prova a pensare a cosa avviene alle cariche sul conduttore quando q si sposta verso di esse...
1) hai una carica Q sulla superficie della sfera conduttrice, se non ci fosse nient'altro questa carica si disporrebbe sulla superficie esterna del conduttore
2) c'è una carica q nel centro della sfera, questa carica produce un campo elettrico centrale che sposta le cariche che sono sulla sfera su un'altra posizione di equilibrio. Ciò vuol dire due cose:
i. la carica totale sulla sfera è sempre Q
ii. il campo elettrico nel conduttore è, ovviamente, zero (altrimenti non sarebbe in equilibrio)
Quindi per il punto (a) devi imporre le condizioni
Dove con
e quello prodotto dalle cariche sulla superficie (che puoi trovare con il teorema di Gauss, considerando una sfera di raggio
Per (b) puoi osservare che per simmetria la forza totale è nulla, mentre per (c) prova a pensare a cosa avviene alle cariche sul conduttore quando q si sposta verso di esse...
Re: SSSUP: Sfera conduttrice con carica puntiforme interna
Bozzio scusa se te lo chiedo ma come sei giunto a  ?
?
Io comunque, piuttosto, direi che per mantenere una differenza di potenziale nulla nella sfera conduttrice, ovvero un campo elettrico a sua volta nullo tra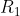 e
e 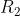 come già detto da Roberto, si viene a creare in
come già detto da Roberto, si viene a creare in 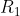 una carica
una carica 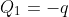 .
.
Per quanto riguarda il punto C, invece, direi che si tratta di un equilibrio indifferente: cambiano le disposizioni delle cariche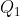 in
in 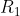 e
e 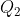 in
in 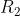 , ma non avviene nulla di più.
, ma non avviene nulla di più.
Io comunque, piuttosto, direi che per mantenere una differenza di potenziale nulla nella sfera conduttrice, ovvero un campo elettrico a sua volta nullo tra
Per quanto riguarda il punto C, invece, direi che si tratta di un equilibrio indifferente: cambiano le disposizioni delle cariche
Re: SSSUP: Sfera conduttrice con carica puntiforme interna
Avevo considerato una sfera di raggio 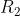 a distanza
a distanza 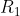 dal centro. In realtà come si dovrebbe fare?
dal centro. In realtà come si dovrebbe fare?
-
Roberto Albesiano
- Messaggi: 8
- Iscritto il: 8 mag 2012, 17:27
Re: SSSUP: Sfera conduttrice con carica puntiforme interna
Cambiano le posizioni delle cariche, appunto: quando la carica q si sposta dal centro verso la superficie della sfera, sulla parte della sfera verso cui si muove si accumula una certa carica di segno opposto a q, che eserciterà una forza attrattiva proprio su di essa. Quindi, dato che su q agisce una forza che la spinge verso la superficie della sfera, direi che l'equilibrio non è indifferente, ma instabile...Andg94 ha scritto:Per quanto riguarda il punto C, invece, direi che si tratta di un equilibrio indifferente: cambiano le disposizioni delle carichein
e
in
, ma non avviene nulla di più.
Non riesco a capire cosa hai fatto (cioè la tua sfera di raggiobozzio ha scritto:Avevo considerato una sfera di raggioa distanza
dal centro. In realtà come si dovrebbe fare?
mentre per il campo prodotto dalla distribuzione di carica
Tra parentesi, mi sono accorto solo ora scrivendo questo (
1) il campo elettrico nel conduttore deve essere zero
2) il flusso del campo elettrico nel conduttore (su una sfera di raggio
3) per il teorema di Gauss allora
Che alla fine è la stessa identica cosa che uguagliare i campi come sopra, ma fatta in mezza riga
Ultima modifica di Roberto Albesiano il 31 lug 2013, 10:08, modificato 1 volta in totale.
Re: SSSUP: Sfera conduttrice con carica puntiforme interna
Si avete ragione ho detto una cavolata. Ma Q_1 non deve essere uguale a -q?
Re: SSSUP: Sfera conduttrice con carica puntiforme interna
Esatto... e, di conseguenza, 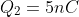 .
.
Re: SSSUP: Sfera conduttrice con carica puntiforme interna
Si però a Roberto viene in modo differente, non ho capito bene il perché. Non ho neanche capito come esplicitare i calcoli che Roberto ha messo sotto forma vettoriale 
Andg potresti spiegare meglio il punto c?
Andg potresti spiegare meglio il punto c?
-
Roberto Albesiano
- Messaggi: 8
- Iscritto il: 8 mag 2012, 17:27
Re: SSSUP: Sfera conduttrice con carica puntiforme interna
Sì avete ragione, ho scritto una cavolata 
Il segno è opposto, quindi viene come avete detto... Chiedo scusa
EDIT: ho corretto i segni nel post precedente
Il segno è opposto, quindi viene come avete detto... Chiedo scusa
EDIT: ho corretto i segni nel post precedente
Ultima modifica di Roberto Albesiano il 31 lug 2013, 10:09, modificato 1 volta in totale.
