Una barra conduttiva di lunghezza
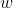
, resistenza

e massa
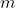
può muoversi senza attrito su due conduttori ideali che si chiudono su un induttore

, e il sistema è immerso in un campo magnetico

uscente perpendicolare al circuito.
a)Considerando l'induttanza nulla trovare l'evoluzione della corrente
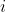
nel tempo se la barra inizia a muoversi con velocità iniziale
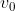
diretta verso destra(esterno del circuito).
b)Che effetto ha l'introduzione dell'induttore L sulla dinamica della corrente nel circuito?
Questo problema mi è sembrato relativamente standard per essere un SNS e ho voluto provarlo, ma non penso di averlo risolto correttamente, soprattutto il punto b.
a) Per la legger Faraday la corrente indotta istantanea a è data da
}{\text{d}t})
e circola in verso orario, inoltre si vede facilmente che quando la sbarretta di muove di un tratto
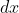
il flusso del campo magnetico varia come
=Bw{d}x)
.
La barra è soggetta poi alla forza di interazione magnetica diretta verso sinistra(interno del circuito)
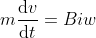
, e unendo queste tre equazioni si ottiene
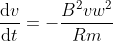
, da cui integrando e consideranzo che in
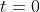
si ha
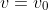
ottengo
=v_0e^{-\frac{B^2w^2}{Rm}t})
, da cui
=\frac{Bwv_0}{R}e^{-\frac{B^2w^2}{Rm}t})
.
b) Qui mi verrebbe da usare direttamente la formula della legge di Faraday con l'induttanza
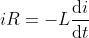
da cui integrando e considerando (ma qui penso di sbagliarmi)
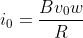
trovo
=\frac{Bv_0w}{R}e^{-\frac{R}{L}t})
, ma mi sembra troppo scontato per essere giusto.
