Trovare la forza necessaria per estrarre quello più piccolo.
81. Solenoidi incastrati
81. Solenoidi incastrati
Un solenoide è stato parzialmente inserito all'interno di un altro. In entrambi scorre una corrente 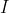 e generano un campo magnetico nella stessa direzione. Entrambi hanno
e generano un campo magnetico nella stessa direzione. Entrambi hanno 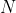 spire e lunghezza
spire e lunghezza 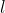 , mentre le sezioni sono rispettivamente
, mentre le sezioni sono rispettivamente 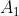 e
e 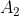 , con
, con  .
.
Trovare la forza necessaria per estrarre quello più piccolo.
Trovare la forza necessaria per estrarre quello più piccolo.
Re: 81. Solenoidi incastrati
Proverei a ragionare con la densità di energia magnetica ] B^2) dove
dove 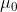 è la permeabilità magnetica e
è la permeabilità magnetica e I) il vettore induzione. Inseriti o no ci sono le energie dei due solenoidi date dalla densità per il loro volume. Ma c'è poi l'energia della parte inserita, diciamo L-x, del più piccolo in cui è presente l'induzione 2B. L'energia magnetica di questa zona mi verrebbe
il vettore induzione. Inseriti o no ci sono le energie dei due solenoidi date dalla densità per il loro volume. Ma c'è poi l'energia della parte inserita, diciamo L-x, del più piccolo in cui è presente l'induzione 2B. L'energia magnetica di questa zona mi verrebbe  = 2\mu_0. N^2.I^2.A_2.[(L-x)/L^2]) . Ora la forza del campo è
. Ora la forza del campo è  per cui quella necessaria esterna è
per cui quella necessaria esterna è 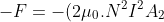/L^2)
Ultima modifica di rocco il 2 lug 2016, 11:23, modificato 1 volta in totale.
Re: 81. Solenoidi incastrati
Ragionare con l'energia è un'idea corretta, ma manca un "pezzo di energia" che non hai considerato 
Re: 81. Solenoidi incastrati
Si è quella della parte esterna x e quindi il coefficiente numerico di F non è -2 ma -3/2 ?
Re: 81. Solenoidi incastrati
Diciamo che c'è un altro tipo di energia da considerare oltre quella immagazzinata nel campo 
Re: 81. Solenoidi incastrati
Comunque quella che ho aggiunto doveva essere aggiunta? E poi io penserei che la variazione di flusso nel piccolo induce in esso una fem e quindi un campo che si oppone all'estrazione con conseguente incremento della forza necessaria: puoi dirmi per favore se sono sulla strada giusta? Perchè stento a quantificarlo anche per il tempo limitato per concentrarmici. Grazie.
Re: 81. Solenoidi incastrati
La parte che hai aggiunto é giusto aggiungerla. Forse però manca ancora un pezzo di energia dovuta al campo che non hai considerato, non ne sono sicuro perché la formula che hai scritto per ) non mi torna dimensionalmente e non vorrei che ci sia un errore di battitura (ho inteso le virgolette come un 2)
non mi torna dimensionalmente e non vorrei che ci sia un errore di battitura (ho inteso le virgolette come un 2) 
Il flusso varia, esattamente, è questa l'altra energia che intendevo
Il flusso varia, esattamente, è questa l'altra energia che intendevo
Re: 81. Solenoidi incastrati
Si le virgolette sono un 2 per errore di battitura dato che nella tastiera sono m e M nella stessa posizione. Inoltre avevo trascurato l'esponente 2 a L al denominatore. In queste giornate ne combino una dietro un'altra...Con questa precisazione dovrebbe tornare dimensionalmente essendo una densità d'energia per un volume. Quando ho un minuto, forse in giornata, cercherò di postare il pezzo induzione che ho già appuntato indicando la lunghezza con l e l'induttanza del solenoide con L. Grazie di tutto.
Re: 81. Solenoidi incastrati
Sempre considerando l-x la parte inserita con l lunghezza del solenoide, estraendo una lunghezza infinitesima dx nel tempo dt si provoca una variazione di flusso dell'induzione generata dal solenoide fisso uguale a ]/dt = A_2.B_1.(N/l)(dx/dt)) , con
, con .I) , che risulterà uguale all'opposto della fem indotta
, che risulterà uguale all'opposto della fem indotta) dove
dove .A_2) è l'induttanza del solenoide. Eliminando il denominatore dt ed integrando fino ad l-x si ottiene la corrente i indotta durante l'estrazione della parte l-x che risulta
è l'induttanza del solenoide. Eliminando il denominatore dt ed integrando fino ad l-x si ottiene la corrente i indotta durante l'estrazione della parte l-x che risulta/(lL)) . Essa corrisponde all'energia
. Essa corrisponde all'energia Li^2= (1/2L)A_2^2.B_1^2.N^2[(l-x)^2/l^2]) fornita dalla forza F che ha compiuto il lavoro di estrazione. La sua derivata corrisponde a questa forza esercitata dall'esterno e dovrebbe risultare, sostituendo anche le espressioni di
fornita dalla forza F che ha compiuto il lavoro di estrazione. La sua derivata corrisponde a questa forza esercitata dall'esterno e dovrebbe risultare, sostituendo anche le espressioni di 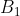 ed L
ed L
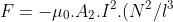(1-x/l))
A parte eventuali errori concettuali ce ne saranno di calcolo?
A parte eventuali errori concettuali ce ne saranno di calcolo?
Re: 81. Solenoidi incastrati
Mi scuso per la risposta molto in ritardo  , il risultato è sbagliato dovrebbe essere indipendente da
, il risultato è sbagliato dovrebbe essere indipendente da  . Sei sicuro che il flusso vari soltanto nel solenoide fisso?
. Sei sicuro che il flusso vari soltanto nel solenoide fisso? 

