Consideriamo un cilindro orientato con l'asse coincidente con l'asse x in assenza di gravità riempito di gas le cui estremità sono mantenute alle temperature
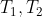
con

. Nella situazione di equilibrio le molecole non stanno accelerando verso una direzione privilegiata: la pressione è uniforme all'interno del cilindro.
Utilizzeremo la formula di Fourier
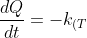}A \frac{dT}{dx} )
dove la conduttanza termica è quella di un gas perfetto a temperatura

, data da
}= \frac{n<v>\lambda C_V}{3N_A})
;
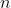
è la densità volumica di particelle e
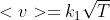
la loro velocità media.
La dipendenza
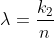
del libero cammino medio da
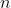
permette di scrivere
}=a \sqrt{T})
ricordando l'espressione della velocità media delle particelle in un gas.
Nella situazione considerata
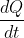
è costante e serve a mantenere il gradiente di temperatura presente. La relazione di Fourier può essere scritta come:
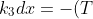^\frac{1}{2}dT)
.
Consideriamo il punto dell'asse del cilindro a
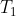
in corrispondenza dell'origine degli assi.
Integrando tra
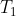
e
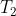
ricaviamo
)
.
Integrando tra
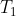
e
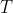
otteniamo finalmente
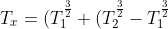\frac{x}{L})^\frac{2}{3})
.
Lo stesso procedimento confermerebbe l'ultima parte della risposta di PG93 se la capacità termica di un gas ideale fosse costante, ma non è così.
A questo punto dall'equazione di stato dei gas perfetti possiamo ricavare
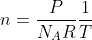
: all'aumentare di x questo diminuisce. Ciò corrisponde ad una maggiore concentrazione di particelle nelle regioni più fredde, come ci aspettiamo.
Nei solidi la conduzione è dovuta a vibrazioni e urti tra molecole e diffusione e urti di elettroni liberi, nei fluidi per collisione e diffusione di molecole, però oltre a dare una conduzione di calore pessima (eccezioni sono l'Elio e l'Idrogeno) non credo che invalidi l'equazione di Fourier.
