0)Un modo banale per dimostrare la formula del periodo è con la terza legge di Keplero. Ovviamente si può fare anche senza darla per scontata.
1)L'equazione differenziale del sistema a due corpi si risolve. Questa cosa è da tenere presente. Per risolverla ci vogliono un po' di trucchetti, perciò non vi consiglio di provarci da zero se non avete mai visto nulla del genere. In fondo a questo messaggio spiego sinteticamente (per quanto è possibile...) come si risolve. Comunque, risolvendola, se

è il momento angolare e
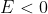
è l'energia, che si conserva, si trova un'ellisse di equazione (in coordinate polari):
)
con eccentricità:

2)Per calcolare l'area percorsa dal raggio vettore in un breve intervallo di tempo
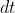
, abbiamo che:
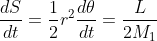
(verifica: avete capito ogni passaggio?). Perciò, integrando su un periodo e usando che l'area dell'ellisse è

:

Servono quindi alcune proprietà dell'ellisse. Si ha che
)
(è una di quelle cose abbastanza facili da dimostrare mettendosi a fare il lavoro sporco con il teorema di pitagora); usando questo, e ricavando

dall'eccentricità che è scritta sopra, si ottiene la formula del periodo.
Riguardo all'energia, si scrive la conservazione dell'energia e del momento angolare all'afelio e al perielio e si fanno i conti.
Soluzione dell'equazione differenziale.
Avvertenza: questa parte è molto difficile per il livello che si prevede in questo forum. È necessario sapere un po' di analisi, e si fa un uso piuttosto pesante delle coordinate polari e delle equazioni differenziali. Non è richiesto che sappiate risolvere la soluzione di questo problema alle Olimpiadi nè ai concorsi di ammissione per l'Università. Io la riporto perchè penso che questo sia un argomento interessante, e spero che riusciate a capirla. Se avete dei dubbi chiedete liberamente, ma se non avete mai sentito nominare la parola "derivata" questa parte probabilmente non fa per voi: non c'è nulla di male.
Vogliamo studiare l'orbita del corpo di massa
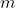
intorno al corpo di massa
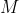
, e assumiamo per semplicità
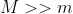
e che il corpo più massivo sia fermo. Vogliamo risolvere il problema in coordinate polari. Poniamo l'origine in coincidenza del centro di forze.
Notiamo innanzitutto che il momento angolare

rispetto all'origine si conserva, perchè l'unica forza agente su
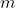
è centrale. Questo implica che il moto del corpo si svolge su un piano. Perciò sono sufficienti due coordinate.
Scegliamo di prendere il versore
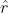
diretto dall'origine a
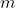
, e il versore
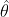
perpendicolare a
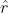
, giacente sul piano del moto e con il verso tale che gli angoli siano positivi se misurati in senso antiorario. Indico con

e

le coordinate dell'angolo.
La posizione del corpo è data da:

(0)
Si può dimostrare che valgono le seguenti relazioni:


Utilizzando queste relazioni, derivando due volte la (0) è possibile ricavare l'accelerazione del punto nella forma:
 \hat{r} + (2 \dot{r} \dot{\theta} + r \ddot{\theta}) \hat{\theta})
La forza che agisce sul corpo è la forza dovuta alla gravità. Ponendo
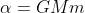
, si ha:
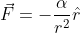
E usando
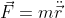
, nelle direzioni radiale e tangenziale, abbiamo:
)
(1)
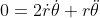
La seconda equazione equivale alla conservazione del momento angolare

. La (1) è l'equazione differenziale da risolvere. Per utilizzare il momento angolare

lo esprimiamo come:

E da questo ricaviamo le due seguenti identità (la seconda è una identità tra due operatori, ma potete anche considerarla come una identità tra due grandezze vere e proprie considerando
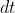
e
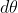
molto piccoli):

(2)

(3)
Si può adesso tornare all'equazione differenziale (1):
 = - \frac{\alpha}{r^2})
Si ricava
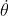
dalla (2), e svolgendo alcuni calcoli si ottiene:

Adesso si vuole usare la (3); la si usa per sostituire la prima derivata temporale con una derivata rispetto all'angolo, portando fuori le costanti dalla seconda operazione di derivazione, ed ottenendo:
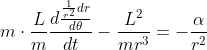
Facendolo di nuovo per eliminare la seconda derivata temporale e svolgendo alcuni calcoli si ottiene:
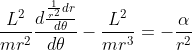
In questo modo ci siamo ricondotti ad una equazione differenziale (apparentemente molto brutta) che coinvolge solo

e

. Risolvendola, troveremo la relazione tra le due coordinate e quindi la forma dell'orbita.
Per risolverla, effettuiamo la sostituzione

. Notiamo che si ha

, perciò l'equazione differenziale si semplifica molto e diventa:
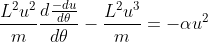
Portando il segno meno fuori dalla derivata e svolgendo alcuni calcoli si giunge all'equazione:

Che è formalmente uguale all'equazione del moto armonico con centro spostato dall'origine. La soluzione è del tipo:
))
Si può dimostrare che questa è l'equazione di una conica (ellisse, parabola, iperbole) in coordinate polari, avente un fuoco nell'origine ed eccentricità

.
A questo punto non è troppo difficile ricavare

in funzione dell'energia e degli altri parametri, perciò, se siete riusciti a capire fin qui, vi consiglio di provarci e provare ad esporre il vostro procedimento.
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
