308. Carica e sfera conduttrice

[Higgs]

Una carica puntiforme q è posta a distanza R dal centro di una sfera metallica di raggio r<R. La sfera è isolata ed elettricamente neutra.
a) Trovare il potenziale elettrostatico sulla superficie della sfera
b) Trovare modulo direzione e verso della forza agente sulla carica

[Pigkappa]

Sembriamo bloccati... Posta un hint per favore, o se vuoi lo posto io. Suggerirei di dare un hint dettagliato, che permetta di arrivare al trucco che serve a risolverlo anche chi non lo ha mai visto.

[Higgs]

Si raccolgo volentieri l'invito anche se non sono trascorsi tanti giorni dalla proposta. Si intuisce che la carica induce cariche di segno opposto nella parte più vicina del conduttore e dello stesso segno nella parte più lontana in modo da generare un potenziale costante sulla superficie sferica. Sarebbe estremamente complesso individuare la distribuzione delle cariche indotte. Si usa allora il cosiddetto "metodo della carica immagine". Ovvero quello di far equivalere la distribuzione indotta a cariche puntiformi interne alla sfera e disposte sul segmento che congiunge q con il centro della sfera. Consiglio di cominciare dal caso in cui la sfera è collegata a terra per cui il potenziale sulla sua superficie è nullo. Si tratta di individuare la carica q', di segno opposto a quello di q, e la sua posizione sulla congiungente. Due incognite e due equazioni ottenute imponendo che il potenziale per es. nei due estremi del diametro sulla congiungente (facilmente calcolabile) sia nullo. La ragione di q' è semplice: in questo caso q si trova di fronte a un conduttore enorme, la sfera e la terra, in cui la parte più vicina è la sfera che quindi si carica negativamente.
Usiamo questi valori quando ci riferiamo al caso in questione della sfera isolata e scarica. Si tratta di determinare una ulteriore carica q'' di segno uguale a quello di q, posta nel centro della sfera....risulterà un potenziale costante sulla superficie sferica che si determinerà agevolmente sfruttando i risultati precedenti.

[matteofisica]

Posto che è la prima volta che tento un problema con le cariche-immagine, provo a dare una soluzione!

Prima di tutto consideriamo il caso della sfera messa a terra: il potenziale deve essere zero su tutta la superficie del conduttore. Ponendo l'origine del sistema di riferimento nel centro della sfera, calcolo l'espressione del potenziale in A(r,0) e in B(-r,0).
e 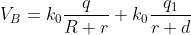, dove ho indicato con d la coordinata x della carica 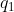. Ponendo uguali a zero entrambe le equazioni si ottiene un sistema 2x2 che dà come soluzione: .
Ora, sfruttando il principio di sovrapposizione, bisogna trovare la carica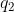 per cui la sfera è isolata e di carica netta 0. Ciò può essere fatto ponendo nell'origine una carica 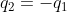, che genera un potenziale uniforme su tutta la superficie sferica pari a .
La forza che viene esercitata su q è data dalla somma vettoriale delle forze (dirette entrambe lungo l'asse x) dovute alle due cariche.
, diretta dunque verso le x negative.

[Francesco Leccese]

Mi hai battuto sul tempo, ma i miei risultati sono gli stessi. Aspettiamo comunque conferma da Higgs

[Higgs]

Bravissimi i risultati sono corretti! Comunque la staffetta va a Matteofisica che ha preceduto Leccese di poco più di un'ora.
Tuttavia penso di essere un pessimo suggeritore. Ho preso troppo alla lettera il consiglio di Pigkappa dando un hint troppo dettagliato. Dopo tutto dobbiamo imparare e si impara poco se uno quasi ti dice come si risolve....Mi consola che Matteo (e presumo anche Leccese)non aveva prima mai risolto un problema con il metodo della carica immagine e dunque almeno questo per lui era nuovo

[Pigkappa]

La soluzione sopra funziona nel senso che dà il risultato giusto... Ma proporrei come punto bonus quello di aggiungere tutti i dettagli che servono per convincere uno studente che non ha mai visto prima questo metodo.
Quindi aggiungerei due componenti:

1. Dimostrare che la superficie del conduttore è tutta allo stesso potenziale.
2. Dimostrare che questa è l'unica soluzione possibile che rispetta le condizioni di potenziale uniforme per la sfera, e di zero carica sulla sfera.

[matteofisica]

Per quanto riguarda il punto 1., direi che si può sfruttare il principio di sovrapposizione degli effetti. Abbiamo una configurazione di tre cariche, due delle quali, q e q1, danno potenziale nullo su tutta la superficie del conduttore. Dunque il potenziale sarà dovuto soltanto alla carica 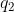. Applico il teorema di Gauss per il campo elettrico a una superficie sferica di centro in 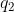e raggio . Il campo elettrico, come è noto, vale 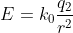. Ricordando ora che il campo elettrico è la derivata (a meno del segno) del potenziale e ponendo il potenziale all'infinito pari a zero, si ottiene l'espressione riportata nella soluzione. Questa dipende da , per cui tutti i punti con la stessa distanza dal centro 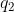si trovano allo stesso potenziale. Segue che la superficie del conduttore (che coincide con la nostra gaussiana) è tutta allo stesso potenziale.
Un altro modo per dimostrarlo è procedere per assurdo: dopo un certo tempo da quando la carica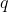 è stata posta nelle vicinanze del conduttore, l'induzione di cariche si arresta e si giunge a una configurazione di equilibrio elettrostatico. Ma se la superficie del conduttore non fosse tutta allo stesso potenziale, vorrebbe dire che le cariche potrebbero migrare su di essa, portandosi verso i punti a potenziale maggiore. Questo va contro l'ipotesi di equilibrio elettrostatico, conducendo a contraddizione. Dunque, la superficie del conduttore deve essere equipotenziale.
Spero di aver detto tutto giusto e di non aver equivocato la richiesta...
Se così non è, passo a lavorare sulla seconda.

[Pigkappa]

Due delle quali, q e q1, danno potenziale nullo su tutta la superficie

A me sembrava mancasse questo passaggio; lo abbiamo dimostrato solo sul punto della sfera più vicino e quello più lontano.

[matteofisica]

D'accordo. Allora provo a dimostrare che, se , allora il potenziale è pari a zero su tutta la sfera. Considero nel piano x,y un punto P di coordinate . Il potenziale in questo punto vale .
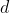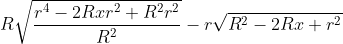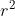Sostituendo tutto ciò che conosciamo e svolgendo i conti, otteniamo: . Considero ora solo il numeratore: ricordando l'espressione di , si ottiene alla fine . Ora, se nel primo termine semplifichiamo per e raccogliamo fuori dalla radice, si ottiene esattamente il secondo termine. Dunque la differenza fa zero, per cui il potenziale in P è zero.
Lo stesso ragionamento si può applicare in tre dimensioni, e ciò dovrebbe provare la tesi.

Ammetto di non essere troppo soddisfatto di questa dimostrazione... c'è un motivo più profondo che dovrei cercare?