Non credo corrisponda alla soluzione a cui stavi pensando, ma pare funzionare
In un sistema di assi cartesiani paralleli alle tre facce, supponiamo che la particella si sposti di
)
e calcoliamo il campo elettrico parallelo ad esso al primo ordine. Consideriamo il parallelepipedo rettangolo centrato nella carica, di lati
 )
, tale che tre delle sue facce coincidano (parzialmente) con quelle del cubo; per simmetria, la forza che esso esercita sulla carica sarà nulla, quindi basta considerare la forza data dalla parte restante del cubo.
Possiamo scomporre la carica rimasta in 3 parallelepipedi di spessore infinitesimo (rispettivamente di lati
)
,
)
,
)
, tre parallelepipedi con due lati di lunghezza infinitesima e un ultimo parallelepipedo con 3 lati infinitesimi. Questi ultimi daranno solo contributi al secondo ordine o più alto al campo elettrico, quindi possiamo trascurarli.
Calcoliamo la componente del campo generato dalla prima "lastra" lungo la direzione di movimento della carica: Si avrà
}^{\frac{1}{2}a-\delta r \sin \theta}\int_{-(\frac{1}{2}a-\delta r \cos \theta \sin \phi)}^{\frac{1}{2}a-\delta r \cos \theta \sin \phi}\frac{\textup{d}z\textup{d}y\textup{d}x}{x^2+y^2+z^2}\frac{(x,y,z)\cdot (\cos \theta \cos \phi, \sin \theta, \cos \theta \sin \phi)}{\sqrt{x^2+y^2+z^2}})
dove si è sfruttato il fatto che il coseno dell'angolo tra due vettori è
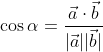
Al primo ordine, l'integrale diventa
^{3/2}}(x\cos \theta \cos \phi+y\sin \theta+z \cos \theta \sin \phi))
Tuttavia, si ha
^{3/2}}(y\sin \theta +z \cos \theta \sin \phi)=0)
visto che stiamo integrando funzioni dispari su un dominio pari.
Ci resta da calcolare l'ultimo termine, ovvero
^{3/2}})
Notando ancora che il dominio è pari, sostituendo
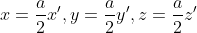
, diventa
^{3/2}}\right ))
Si può dimostrare (in un secondo post
) che il doppio integrale tra parentesi vale
^{3/2}}=\frac{1}{x'} \tan^{-1}{\frac{1}{\sqrt{(x'^2+1)^2-1}})
Inoltre, dal teorema fondamentale del calcolo integrale si ha, al primo ordine,
\textup{d}t=2f(1)\delta x)
Quindi, vale
^2-1}}=\frac{2\rho \cos^2\theta\cos^2\phi}{\pi \varepsilon_0}\tan^{-1}{\frac{1}{\sqrt3}}\delta r=\frac{\rho \cos^2\theta\cos^2\phi}{3 \varepsilon_0} \delta r)
Analogamente, si otterrà
,
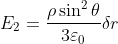
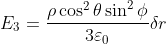
, quindi la forza esercitata sulla carica vale
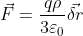
Infine, si trova facilmente che la frequenza delle piccole oscillazioni vale
.
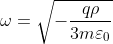
, avente una densità di carica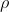 
costante e uniforme. Una particella puntiforme di massa 
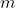e carica 
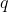, tale che 
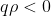, è costretta a muoversi lungo una retta fissa passante per il centro del cubo, senza alcun tipo di attrito. Si trovi il periodo delle sue piccole oscillazioni attorno al centro del cubo.
