Scusa se rispondo solo adesso ma ho avuto un po'da fare in questi giorni.
Il fatto che la corrente tra

e
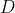
è uguale in modulo e verso a quella tra
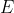
e

è dato dalla simmetria destra/sinistra del circuito ma non ti dà nessuna informazione sui potenziali di
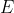
e
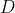
se non che siano opposti ma potrebbero non essere nulli (cosa che effettivamente succede).
Il ragionamento in due tempi mi piace abbastanza (è necessario formalizzarlo meglio, prova a pensare alla sovrapposizione degli effetti) come si distribuiscono le correnti quando escono dal nodo

e come rientrano dal nodo

prova a pensarci ancora un po'
la resistenza equivalente tra i nodi
e
la resistenza equivalente tra i nodi
e
la resistenza equivalente tra i nodi
e
se il filo tra essi viene tagliato