Pagina 1 di 2
89. Carica immagine
Inviato: 11 ago 2016, 17:18
da BeppeBogna
Mi è stato dato l'arduo compito di continuare la staffetta, propongo questo problema

Una carica
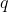
è posta nelle vicinanze di una sfera metallica neutra, di raggio

e collegata a terra a distanza
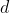
dal suo certo. Si sa che sulla sfera si induce una certa distribuzione di cariche, che all'esterno di essa produce lo stesso campo elettrico di una carica
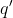
sulla congiungente tra la carica e il centro, a distanza
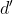
da quest'ultimo.
1) Esprimere
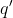
e
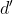
in funzione di
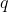
,

e
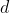
.
2) Trovare l'energia elettrostatica dovuta all'interazione tra
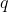
e le cariche indotte.
3) Trovare l'energia elettrostatica dovuta all'interazione tra le cariche indotte.
Un corpo puntiforme di massa
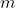
e carica
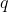
è appeso a un filo di massa trascurabile lungo

, attaccato al soffitto. Il centro di una sfera metallica neutra, di raggio

e collegata a terra si trova esattamente sulla verticale del punto di contatto tra il filo e il soffitto, a distanza
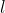
da quest'ultimo.
4) Trascurando la forza gravitazionale e ogni tipo di attrito, calcolare la frequenza delle oscillazioni della massa
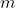
, quando questa viene spostata di un piccolo angolo

dalla verticale.
Re: 89. Carica immagine
Inviato: 12 ago 2016, 11:04
da DEhunt
Posso chiederti cosa implica il fatto che sia collegata a terra? Nel senso, cosa cambierebbe se non lo fosse?
Re: 89. Carica immagine
Inviato: 12 ago 2016, 15:30
da BeppeBogna
Serve solo a semplificare i calcoli, concettualmente a poco.
Re: 89. Carica immagine
Inviato: 12 ago 2016, 17:26
da rocco
Provo a dare i primi tre risultati, se andranno darò il quarto
1)


imponendo il potenziale nullo in due opportuni punti della superficie sferica
2)

come energia di interazione fra due cariche puntiformi
3)

energia conduttore sferico di carica q' e capacità

Re: 89. Carica immagine
Inviato: 12 ago 2016, 21:23
da BeppeBogna
Nel punto 1) probabilmente ti sei perso un segno, è
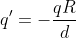
, quindi anche l'energia al punto 2) ha segno opposto, per cui puoi postare i procedimenti.
L'energia al punto 3) è sbagliata invece, ritenta

Re: 89. Carica immagine
Inviato: 13 ago 2016, 11:45
da rocco
1) si mi ero perso il segno perchè con q' indicavo il modulo e quindi l'energia era giusta 2) considerando invece q' con segno allora in effetti l'energia ha segno complessivamente negativo come deve essere 3) ripenserò, ma le cariche q' sono sulla superficie sferica in realtà e quindi mi pareva il classico conduttore isolato per quanto riguarda le cariche indotte. Perchè sbaglio?
4) mentre ripenso al 3), ti darei il mio risultato: la forza elettrica di attrazione mi verrebbe
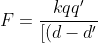^2+L^2.\alpha^2})
. Trovandone la componente tangente alla circonferenza come nel pendolo, cioè moltiplicando per
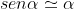
e trascurando a denominatore l'infinitesimo di secondo ordine si arriva all'equazione
^2}=0)
dove si osserva che il segno del secondo addendo al primo membro è positivo e quindi il moto è armonico. Da
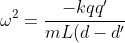^2})
si ricaverebbe per la frequenza
}{2\pi.(d-d')\sqrt(mL)})
dove
^2-R^2]/(l-L))
Ci sta che abbia fatto errori?
Re: 89. Carica immagine
Inviato: 13 ago 2016, 14:43
da BeppeBogna
Attento a non approssimare troppo! L'equazione della forza è quasi giusta, ma devi anche tener conto del fatto che mentre
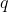
oscilla (e quindi varia la sua distanza dal centro della sfera) variano anche il valore e la posizione di
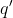
. Però sei comunque sulla buona strada

Per quanto riguarda l'energia, in un conduttore sferico con quella capacità se non sbaglio fai l'implicita assunzione che la carica sia uniformemente distribuita sulla superficie, cosa che qui non accade.
Re: 89. Carica immagine
Inviato: 14 ago 2016, 10:10
da rocco
Si, hai ragione non è distribuita uniformente. Allora la vedo così: siccome il potenziale deve essere nullo in tutti i punti della sfera e quindi anche nella posizione occupata da q', ricaverei che il potenziale delle cariche distribuite sulla sfera (non importa sapere come) deve essere opposto a q/(d-d'). L'energia di interazione-indotte sarebbe questo potenziale per q' ovvero
(-qq')/(d-d'): mi verrebbe opposta all'altra! A ripensarci però mi sembra verosimile perchè deve essere positiva ed in definitiva è q che provoca tutto. Che ne pensi?
Per il punto 4), aderendo al suggerimento e in definitiva esprimendo q' in funzione di q perchè la distanza era già espressa con i dati certi (l-L) e R, otterrei
}}{2\pi.[(l-L)^2-R^2]\sqrt{mL}})
dove gli errori di calcolo sono sempre in agguato.
Re: 89. Carica immagine
Inviato: 14 ago 2016, 17:46
da BeppeBogna
La frequenza ora va quasi bene, probabilmente hai solo fatto un errore di calcolo e non dovrebbe esserci

nel numeratore sotto radice. Sull'energia ancora non ci siamo, più che altro per il fatto che il potenziale dovuto alle cariche indotte deve essere punto per punto opposto a quello di
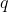
come dici tu, ma quest'ultimo potenziale varia a seconda del punto considerato della sfera. Se entro un paio di giorni nessuno riesce a trovare qualcosa, darò qualche hint.

Re: 89. Carica immagine
Inviato: 15 ago 2016, 11:22
da rocco
E' per questo che avevo considerato proprio il potenziale di q nel posto occupato da q': il potenziale delle indotte in quel punto deve essere opposto a questo potenziale e dunque non capisco l'errore

Continuerò a pensarci in questi giorni prima del test

e spero di capirlo prima dell'hint o di qualche soluzione.
Ho un'altra idea che posto domani.
Sul previsto errore di calcolo, se il procedimento è giusto, francamente non ci perderò tempo.

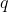 è posta nelle vicinanze di una sfera metallica neutra, di raggio
è posta nelle vicinanze di una sfera metallica neutra, di raggio  e collegata a terra a distanza
e collegata a terra a distanza 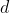 dal suo certo. Si sa che sulla sfera si induce una certa distribuzione di cariche, che all'esterno di essa produce lo stesso campo elettrico di una carica
dal suo certo. Si sa che sulla sfera si induce una certa distribuzione di cariche, che all'esterno di essa produce lo stesso campo elettrico di una carica 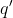 sulla congiungente tra la carica e il centro, a distanza
sulla congiungente tra la carica e il centro, a distanza 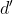 da quest'ultimo.
da quest'ultimo.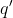 e
e 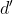 in funzione di
in funzione di 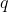 ,
,  e
e 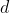 .
.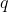 e le cariche indotte.
e le cariche indotte.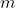 e carica
e carica 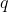 è appeso a un filo di massa trascurabile lungo
è appeso a un filo di massa trascurabile lungo  , attaccato al soffitto. Il centro di una sfera metallica neutra, di raggio
, attaccato al soffitto. Il centro di una sfera metallica neutra, di raggio  e collegata a terra si trova esattamente sulla verticale del punto di contatto tra il filo e il soffitto, a distanza
e collegata a terra si trova esattamente sulla verticale del punto di contatto tra il filo e il soffitto, a distanza 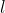 da quest'ultimo.
da quest'ultimo. 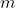 , quando questa viene spostata di un piccolo angolo
, quando questa viene spostata di un piccolo angolo  dalla verticale.
dalla verticale.