Forum OLIFIS

Propongo qiesto problema che non riesco a risolvere completamente... Consideriamo un proiettile lanciato dall'origine in una direzione formante un angolo \alpha con il piano orizzontale; la sua posizione successiva sia r(t). Per angoli abbastanza piccoli la distanza dall'progine aumenta sempre. Per angoli vicini a 90°, invece, il proiettile salendo dapprima si allontana dall'origine e poi scendendo si avvicina nuovamente.
Quale angolo critico \alpha suddivide le due classi di lanci?

Io l'ho interpretato come una distinzione tra i lanci dove nel primo caso il punto più distante dall'origine è il punto finale della traiettoria e nel secondo caso invece un generico punto della traiettoria... Io mi sono fermato a stabilire se il punto di arrivo è più lontano del vertice della parabola o no... Diciamo che la mia è una soluzione parziale ma dal testo credo che bisogna trovare altro... Ho fatto qualche deduzione su come si allontana il proiettile e per esempio che se da un certo punto in poi si riavvicina allora continuerá a farlo fino alla fine... Solo che se se il proiettile ricomincia ad avvicinarsi durante la discesa magari ho escluso alcuni angoli... che fare?
Scusate la mancanza di latex e altro ma senza computer non posso fare cose ottime

Indichiamo con la posizione del proiettile rispetto all'origine (cioè il punto da cui è partito) nel piano in cui si muove (che mi sembra sia la stessa notazione che hai usato tu): il proiettile si riavvicina all'origine se il modulo di questo vettore ha un massimo, distinto dal punto di arrivo, tra la partenza e il punto di arrivo appunto.
Quindi, sapendo le due componenti su x e y di , possiamo calcolarne il modulo:




Una volta che conosci un'espressione per il modulo di ne studi la crescenza e la decrescenza al variare di : guardi per quali angoli c'è il massimo e per quali no e quindi dovresti trovare l'angolo limite che cerchi. Ti torna?

Devo usare l'analisi?
Proverò... devo porre la derivata uguale a zero per trovare il punto di massimo?

Simone256 ha scritto:Devo usare l'analisi?
Proverò... devo porre la derivata uguale a zero per trovare il punto di massimo?

Sì, direi che usare l'analisi è l'unico modo... Comunque è meglio se qualcosina di analisi la impari perché può sempre tornare utile.
Ponendo la derivata uguale a zero trovi sia i massimi che i minimi, quindi occhio. Di solito si studia il segno della derivata per capire quali sono massimi e quali minimi (in spicci, se la derivata passa da negativa a positiva è un minimo, se passa da positiva a negativa è un massimo). Comunque, ripeto, vatti a vedere qualcosa di analisi perché serve parecchio... ciao!

Ci ho provato! Se qualcuno non ha niente da fare potrebbe cortesemente dirmi se il risultatoè giusto?
Mi esce

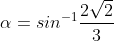
Grazie

Scrivi i tuoi calcoli così è possibile controllarli.
A me viene (potrei aver sbagliato i calcoli)

Si mi viene lo stesso ma mettere qui i calcoli sarebbe un casino perchè fino a domenica non vedl nessun computer...

In ogni caso visto che si parla di analisi ho bisogno di un aiutino....
Una particella si muove lungo l'asse x in modo tale che la sua velocità nella posizione x è data dalla formula v(x)=2+2sin(x) . Qual è la sua accelerazione in x=\pi /6 ???

Dalla formula a=(V^2-v^2)/2S ho pensato di derivare la funzione v^2(x) rispetto a x e poi dividere per 2... Evidentemente non funziona! Come fare?
Il risultato esatto sarebbe .

L'accelerazione è la derivata della velocità, quindi basta derivare v(x) e sostituire la tua x, sei sicuro che il risultato è quello?

Eh ma l'accelerazione non è la derivata della velocitá rispetto al tempo? Io qui ho la velocitá rispetto alla posizione... Poi magari hai ragione perchè ho appena cominciato a studiare analisi :l

Hai ragione avevo visto v ed a e l'ho sparato a cavolo
Comunque avevo pensato di fare cosi, solo non mi esce quel risultato e non sono sicuro della correttezza:
Dato che e che , ho sostituito dt nella seconda ottenendo dove è la derivata di v(x), e quindi .