Forum OLIFIS

Higgs ha scritto: ↑

10 lug 2025, 10:45

Avevo provato ad esprimere il rapporto in funzione dell'ordinata y di C e pensavo di determinarne il massimo annullando la sua derivata prima rispetto a y. Ora il problema è che C avrà anche un'ascissa.. Ho provato a metterci 35 che è la massima possibile ma non torna una cosa verosimile.

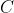
L'ascissa di è ovviamente , in quanto nel sistema considerato il punto di collisione è shiftato solo verticalmente. Dato che il problema è rimasto aperto per molto tempo fornisco un indizio più approfondito. Il massimo del rapporto si ha quando, considerato il triangolo , l'angolo in è retto (prova a dimostrare questo claim). Alternativamente come hai detto puoi approcciarlo come hai scritto, tenendo conto di cosa detto sopra.

Dai miei conti che avevo fatto con l'ascissa di C pari a 35 m e tenendo ora conto che è rettangolo in avrei trovato che l'ordinata di C è uguale a 30 m . Pertanto mi risulterebbe che u è circa il 90% di v.
Vorrei sottolineare un procedimento per dimostrare il claim. Si può calcolare facilmente il rapporto in funzione di numeri e di y, cioè di y. Allora nel massimo del rapporto si dovrebbe annullare la derivata rispetto a y e quindi calcolare y. Perchè non viene 30 m???

L’ordinata del punto ora mi pare corretta, molto buono! Se vuoi concludi i conti e posta il procedimento scritto bene per completezza, da qui non credo ci saranno problemi.

Per determinare la y di C si può valutare applicando il teorema di Pitagora ad un triangolo rettangolo di cui sia ipotenusa e al triangolo rettangolo in . Uguagliando le due espressioni si ricava y essendo le espressioni composte da numeri e y. Riferendoci ai quadrati si trova
da cui l'equazione risolvente in y e quindi y=30 m.

Ora per dimostrare il claim io avevo pensato di determinare il rapporto usando due triangoli rettangoli escludendo ovviamente quello in . Per esempio riferendoci ai quadrati per semplicità e Emerge un rapporto nella incognita y che dovrebbe avere un massimo per x=30 m. Quindi si dovrebbe annullare la derivata prima rispetto a y per y=30. NON SUCCEDE! Perché? Dove è sbagliato questo ragionamento?