Pagina 2 di 3
Re: Tiri al bersaglio
Inviato: 2 lug 2025, 23:10
da Ising
Per quanto riguarda il punto 2 sei sicuro della condizione su
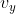
e
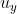
? In particolare ciò che hai scritto dovrebbe implicare che le pietre si scontrano ad
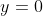
. La scelta del sistema di riferimento in caduta libera è efficace, prova a vedere le forme delle traiettorie (che credo abbia già intuito in ogni caso) delle pietre e la posizione del punto di collisione in questo sistema. Infine credo la cosa migliore sia sostituire alla fine i valori numerici, altrimenti si finisce in espressioni dimensionalmente sbagliate.
Re: Tiri al bersaglio
Inviato: 4 lug 2025, 20:14
da Mangogiallo26
Li dove mi hai evidenziato il messaggio ho sbagliato a non mettere la posizione al tempo 0 del punto di contatto, anche se poi dopo ne ho tenuto conto. Le traiettorie comunque sono due rette e il punto di contatto sta accelerando verso il basso. C’è un modo più intelligente per farlo? perché non vedo dove ho sbagliato la mia soluzione.
Re: Tiri al bersaglio
Inviato: 4 lug 2025, 20:14
da Mangogiallo26
Il punto di contatto accelera verso l’alto scusami. Btw c’è un modo per modificare i messaggi inviati?
Re: Tiri al bersaglio
Inviato: 6 lug 2025, 10:55
da Higgs
Non sono forte nei sdr strani e quindi devo fare la mia osservazione a Mangogiallo 26 per vedere se è corretta. Mi pare che nel riferimento in caduta libera secondo l'asse y, le velocità

dovrebbero annullarsi perchè le pietre cadono insieme al riferimento medesimo. Mi paiono invece giuste le velocità parallele all'asse x. Siccome il tempo t all'impatto in ( 35,12) è lo stesso, dovrebbe essere giusto che, essendo

, sia anche

e quindi

Errori dimensionali non dovrebbero esserci: gli spazi in m, i tempi in s, le velocità in m/s.


Re: Tiri al bersaglio
Inviato: 6 lug 2025, 21:33
da Ising
Scusatemi se il messaggio non verrà formattato molto bene, posso scrivere solo dal telefono al momento. Comunque il fatto che
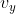
e
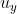
siano nulle nel sistema scelto non è vero, in quanto tale sistema è solo accelerato con

e non solidale al moto verticale delle pietre. Come ha detto Mangogiallo, però, queste rimangono costanti nel tempo e segue la traiettoria rettilinea delle pietre. Come idea carina di soluzione avevo pensato a questo: dico

e

rispettivamente i punti di lancio della pietra sopra e sotto e
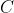
il punto di collisione nel sistema accelerato sempre (si noti come è differente dal punto nel sistema del laboratorio, com’è stato già detto anche). Poiché la

è fissata, il problema è equivalente a massimizzare

. Quando si verifica questo? Una buona idea è farsi un disegno e considerarlo geometricamente, in particolare si può trovare l’ordinata di
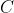
. Da qui il problema si conclude senza molte difficoltà.
Re: Tiri al bersaglio
Inviato: 7 lug 2025, 11:40
da Higgs
A me risulterebbe
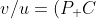/(P_- C)=15/10)
e quindi
 v)


E' sbagliato...?
Re: Tiri al bersaglio
Inviato: 7 lug 2025, 16:53
da Ising
Non mi risulta in realtà. Come hai imposto la condizione di

massimo?
Re: Tiri al bersaglio
Inviato: 7 lug 2025, 17:11
da Higgs
Ho cercato di determinare l'ordinata di C che mi risulta 10 per cui

donde la mia soluzione. I P sono fissi devo determinare C in modo che u sia massimo? Non lo vedo...
Re: Tiri al bersaglio
Inviato: 7 lug 2025, 19:07
da Ising
Poiché l’ordinata del corrispondente a
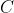
nel sistema del laboratorio è 12, sicuramente non potrai avere

in quanto questo risultato è minore del valore sopra citato. Comunque si, è necessario massimizzare il rapporto “aggiustando” l’ordinata di quel punto. Prova a farlo con un disegno e considerazioni geometriche
Re: Tiri al bersaglio
Inviato: 10 lug 2025, 10:45
da Higgs
Avevo provato ad esprimere il rapporto

in funzione dell'ordinata y di C e pensavo di determinarne il massimo annullando la sua derivata prima rispetto a y. Ora il problema è che C avrà anche un'ascissa.. Ho provato a metterci 35 che è la massima possibile ma non torna una cosa verosimile. Quale ascissa dare a C?


Occorre scomodare la teoria in due variabili con la matrice hessiana per trovare max e min?