Forum OLIFIS

Mi sento di proporre la strada che sto seguendo io se qualcuno mi vuole dare un feedback. Per simmetria ogni gamba supporta un momento massimo rispetto a sè uguale a , dove R è la distanza dal vertice al centro del triangolo equilatero. Se ho una massa , per far sì che il tavolo non si rompa deve valere per ciascuna gamba , dove 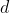è la distanza dal vertice ad un generico punto dove si può appoggiare l'oggetto. Sostituendo la disequazione sopra citata dà . Quindi, considerando un solo vertice, l'area interessata è un settore circolare tangente al triangolo equilatero (per le relazioni tra mediana e baricentro) di raggio 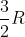. Se adesso consideriamo tutti e tre i vertici e intersechiamo le tre aree si ottiene un triangolo "bombato", che rappresenta tutti i punti in cui è possibile posizionare la massa senza che il tavolo si rompa, di cui è necessario calcolare l'area. Da qui non sono riuscito ad andare avanti, soprattutto perchè non riesco a trovare la parte "bombata" del triangolo. Ha senso ragionare sul momento torcente?

Ma perchè mi chiedi "corrisponde in che senso"? Io ho capito che posto nel centro del triangolo di lato 1 produce una reazione di ciascuna gamba pari a dividendosi il carico sulle 3 gambe; una reazione che è possibile perchè inferiore di alla reazione di rottura che secondo il testo è . Dunque il triangolo dato di lato 1 "corrisponde" a equilibrare senza rompersi nelle gambe . Mi chiedo : qual è il triangolo capace di equilibrare la metà del carico (="corrisponde" alla metà del carico ) posta nel suo centro? E' quello di lato (1/2) capace di equilibrare senza rompere le 3 gambe ovvero 1/3 del carico di rottura posto nel suo centro. La distanza del centro dai suoi vertici è ovviamente la metà invece di e la sua area è come detto in dettaglio nei miei post .
Pertanto le mie risposte, che tu ritieni errate o non convincenti, sono 1) l'area richiesta è un triangolo equilatero simile a quello dato di lato 1; 2) la sua area è Se è sbagliato vuol dire che il valore giusto viene per errori che si compensano o per una mia incomprensione del testo. Da parte mia credo di poter chiudere questo argomento.

Fibdg ha scritto: ↑

11 lug 2024, 16:37

ogni gamba supporta un momento massimo rispetto a sè

Le gambe si rompono se la forza esercitata su di loro è troppo grande, non se il momento torcente è troppo grande... Questo mi pare intuitivo...

Fibdg ha scritto: ↑

11 lug 2024, 16:37

Ha senso ragionare sul momento torcente?

Sì. Tenere conto del momento torcente serve. Le forze esercitate dalle gambe del tavolo saranno tali da impedire che il tavolo ruoti rispetto a qualsiasi asse: equilibrio dei momenti. Ed anche ad impedire che sprofondi nel terreno o si innalzi in volo: equilibrio delle forze.

È vero ho scritto delle scemenze, grazie Pigkappa dei suggerimenti, anche a me ora viene (contacci non ce n'erano ).

Ok ma mantenp o Fidbg, postate una soluzione con spiegazione corretta (o Higgs rivedi la tua così che si capisca la parte fisica), oppure la staffetta non so a chi darla :p

Per me possono andare mantanp o Higgs con le loro soluzioni

Io la soluzione ce l'ho ma sono via e non ho un supporto comodo per scriverla qua. Al massimo posso spiegare come ho risolto il problema, ma per qualche giorno non riesco a scriverla bene.

Per evitare che la staffetta resti bloccata, il primo tra mantenp, Higgs e Fibdg che ha un problema, lo può postare come 323
Metto la mia soluzione qua sotto

Il tavolo sorregge la massa e sente quindi una forza dove si trova la massa.
Le gambe del tavolo, ai vertici A, B e C, esercitano forze sulla superficie del tavolo rispettivamente.

Trascuro il peso della superficie del tavolo, che aggiungerebbe solo una componente a ognuna di .

Poiché la superficie del tavolo non trasla, la somma delle forze è nulla.
Poiché non ruota, il momento torcente delle forze rispetto a qualsiasi asse è nullo.

Prendiamo come asse il lato e calcoliamo i momenti.
Non presto particolare attenzione ai segni ma solo ai moduli.
Il momento di e è zero perché la distanza dall'asse è zero.
Il momento di è dove è la distanza della massa dal lato BC.
Il momento di è dove è l'altezza del triangolo.

Questi si devono equilibrare, quindi , quindi .
Se il corpo è nel centro del triangolo, e troviamo che per simmetria è chiaramente corretto.
Se il corpo è nel punto A, troviamo che è molto plausibile a sua volta.

La forza massima sostenibile è e la forza calcolata è , quindi .
Perciò il corpo non può trovarsi nel triangolino equilatero di lato che ha vertici in A e nei punti medi di AB e AC.

Lo stesso ragionamento esclude gli altri due triangoli simili con vertici in B e C.

Rimane come zona permessa un triangolo equilatero che ha lo stesso baricentro di quello iniziale e lato .
La sua area è un quarto di quella del triangolo iniziale, che calcolo come base per altezza diviso 2: