Sulla definizione di
Relatività ristretta
Re: Relatività ristretta
Inizio con il ringraziarti per la risposta dettagliata. Purtroppo, per mie difficoltà con gli sviluppi, faccio ancora fatica a capire quanto hai scritto nel primo messaggio, nonostante le chiare e corrette considerazioni che mi hai presentato nel tuo ultimo e che mi hanno aiutato molto nel comprendere meglio questo potente strumento matematico. Provo dunque ad esplicitare meglio da dove trae origine la mia confusione rispetto alla definizione di  ed
ed  .
. ) come da te scritta nella prima parte dell'estratto riportato non ho nulla da dire:
come da te scritta nella prima parte dell'estratto riportato non ho nulla da dire: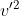 e
e 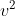 sono nell'ordine corretto rispetto alla definizione generale di sviluppo. Il dubbio sorge tuttavia sulla definizione di
sono nell'ordine corretto rispetto alla definizione generale di sviluppo. Il dubbio sorge tuttavia sulla definizione di ) . Se stiamo utilizzando
. Se stiamo utilizzando 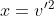 , la derivata non dovrebbe essere fatta proprio rispetto a tale termine? In sostanza non dovrebbe essere:
, la derivata non dovrebbe essere fatta proprio rispetto a tale termine? In sostanza non dovrebbe essere:  = \frac{\partial L(v^2)}{\partial (v'^2)}) ? Grazie ancora.
? Grazie ancora.
-
Tarapìa Tapioco
- Messaggi: 146
- Iscritto il: 30 lug 2023, 15:28
Re: Relatività ristretta
Questa obiezione è veramente molto interessante, in quanto riguarda un punto delicatissimo che necessita di essere affrontato con attenzione. Si deve registrare, cionondimeno, che non vi sia alcuna connessione logico-matematica tra l'oggetto della replica proposta, cioè
, e il risultato di
In tal senso, è doveroso estendere la trattazione sulla Lagrangiana relativistica effettuando una premessa. La forma del tipo
La risposta specifica corretta, in questo caso, è quella che mira a considerare
Quando i matematici affrontano una funzione, la intendono come una regola che consiste nel prendere un input (o una serie di input) e produrre un output. Ad esempio, la regola del "quadrato di". Se
La
I fisici, invece, sono interessati alle relazioni funzionali tra variabili fisiche. Se
Sussiste, in tal senso, una confusione generale sulla regola della catena (chain rule) a più variabili. Il problema è spesso causato da una mancanza di chiarezza sul ruolo delle funzioni e delle variabili e sul significato preciso di ciascuna derivata. A questo scopo, fondamentale si rivela la necessità di una breve trattazione su tale argomento.
Parte A. Regola della catena a una sola variabile.
1) Notazione funzionale
Si inizi con una descrizione della regola della catena in una dimensione, per la quale occorrono due funzioni
Utilizzando
Con le opportune ipotesi su
Si noti che ciò significa: la derivata di
2) Notazione differenziale
La notazione alternativa per la regola della catena, ovviamente, è:
Questa notazione, relativamente agevole e semplice, consente di eseguire rapidamente il calcolo, ma si noti quanta precisione sia stata persa:
1.
2. Si sono persi i punti in cui tali funzioni dovrebbero essere valutate.
3. Cos'è esattamente
Questo è il motivo per cui bisogna stare attenti a utilizzare la notazione differenziale, al fine di non perdere di vista come vengano definiti gli oggetti matematici e quale relazione sia funzione di tal altra. Si noti come l'equazione
Parte B. Regola della catena a più variabili.
Nel caso del calcolo a più variabili, si parta da una funzione
Si noti come la notazione per le derivate parziali sia legata a un particolare insieme di variabili fittizie -
Allora, si ha:
Si noti come queste derivate parziali siano esse stesse funzioni delle tre variabili. In generale, una volta definita
Si noti che, tecnicamente,
L'ambiguità può sorgere, tuttavia, se
allora si è definita una nuova funzione
Cosa è esattamente
In effetti, le condizioni peggiorano. Se semplicemente
e la regola della catena in questo caso restituisce:
dove, tecnicamente,
Per illustrare ciò, si potrebbe, ad esempio, scrivere in maiuscolo le lettere che denotano a quale derivata parziale ci si riferisce quando rappresentino variabili fittizie, e lasciarle nella loro intrinsecità quando descrivano variabili e funzioni specifiche. Questo porterebbe a:
Ciò evidenzia che
Nella notazione differenziale, l'equazione
dove il membro sinistro dell'equazione è spesso chiamato derivata "totale" di
Si noti, tuttavia, come non si tratti veramente di una derivata di
Sebbene l'equazione
Il passaggio chiave in questo processo è il riconoscimento della circostanza per cui si è fatto ricorso ai simboli
Parte C. Esempio di carattere fisico
Per illustrare l'uso della regola della catena a più variabili in un contesto fisico, si consideri una particella sotto un potenziale dipendente dal tempo, definito come una funzione di quattro variabili:
Si noti che spesso i testi adotteranno lo stesso simbolo per entrambe tali funzioni e scriveranno semplicemente:
sovraccaricando il simbolo
oppure, in notazione differenziale:
Questa è la notazione standard, ma si può vedere dalle equazioni
Si noti anche che
Conclusione generale
Una comprensione approfondita della regola della catena a una variabile è un prerequisito importante per il calcolo a più variabili. La regola della catena a più variabili comporta un certo sovraccarico dei simboli
Conclusione specifica
La conclusione più appropriata alla domanda è quella in accordo alla quale non vi è una soluzione totalmente soddisfacente, in quanto si rimane bloccati con la notazione. Nella notazione standard, il problema consiste nel fatto che, riguardo le derivate parziali, non esiste una notazione senza argomenti per la derivata. Non si tratta di un errore, dunque, ma di una carenza nella notazione differenziale.
A sostegno della notazione
Questa argomentazione è errata. ComePer definizione,, qualunque sia
. Poiché si ha
a sinistra, così dev'essere anche nel membro a destra.
Il modo corretto di scrivere l'espressione è
In favore della notazione
La comune convinzione popolare ritiene che la variabile rispetto alla quale calcolare la derivata, presente al denominatore di ogni derivata in notazione differenziale, debba sempre, necessariamente, rappresentare stricto sensu la variabile che cambia, fondamentale per il risultato finale in quanto è proprio in questo punto di spostamento che si vuole calcolare la derivata finale più generale. In molti casi (questo compreso), soprattutto nelle derivate parziali, il denominatore è invece occupato dalle cosiddette dummy variables, variabili fittizie che appaiono in alcuni calcoli solo come marcatori (placeholders, obbedienti solo alla stretta necessità di occupare una posizione) e, relativamente alla determinata operazione (in questo caso, la derivata parziale), scompaiono completamente nel risultato finale non influendo su quest'ultimo.Si consideri una funzionecon un'espansione in serie di Taylor:
Adesso, se si vuole sostituire la derivata con la forma differenziale, cosa usare:oppure
? Preferibilmente sarebbe meglio introdurre
, quale punto variabile, al denominatore della derivata
, in quanto la derivata rispetto ad
sembra strana e include il punto di riferimento (o di valutazione).
 = L(a) + \frac{\partial L(a)}{\partial x}(x-a) + \frac 1 2 \frac{\partial^2 L(a)}{\partial x^2}(x - a)^2 + \dots)
Pertanto, la questione è puramente concernente la notazione: è possibile scrivere, indistintamente,
È dunque importante notare, soprattutto dal punto di vista dell'analisi funzionale, che una funzione è definita indipendentemente da qualsiasi variabile e che una funzione di una sola variabile possiede derivata unica: in questo caso, quindi, l'operatore differenziale è unico. Pertanto, anche se alcune notazioni richiedono una variabile del tipo
Nota. Una funzione si dice ben definita quando bisogna verificare che la definizione fornisca un unico valore output per ogni valore input. Il termine ben definito (in contrapposizione a - banalmente - definito) è tipicamente usato quando una definizione dipende da una scelta solo apparentemente, ma non effettivamente. Nella maggior parte dei casi (ma non in tutti), ciò si applica alla definizione di una funzione
In altri termini, una funzione
1) Per tutti gli
2) Per tutti gli
Il secondo assioma è quello che rende una funzione "ben definita". Non v'è bisogno di addurre alcuna prova per dimostrare che "le funzioni sono ben definite" (infatti, lo sono per definizione), ma molto spesso si dispone di una regola inventata per creare una relazione e si deve dimostrare che "tale relazione ha le proprietà 1) e 2), dunque è una funzione ben definita". Quando si definisce una funzione sull'insieme delle classi di equivalenza
Si consideri la definizione della funzione
Al contrario, se si definisce
Il problema è quello per cui non si possiede una definizione diretta di numeri razionali, che si definiscono invece come classi di coppie di numeri interi
In definitiva, dunque, se si vuole asserire che
1)
2) Il dominio di
3) Nessun elemento di
Dunque, assumere che una relazione sia ben definita significa concludere che tutte e tre le condizioni siano vere. Se si conoscono alcuni di questi requisiti, bisogna solo verificare gli altri: ad esempio, se si conosce che
Se non è dato che
Ultima modifica di Tarapìa Tapioco il 25 dic 2023, 12:36, modificato 13 volte in totale.
Re: Relatività ristretta
Esistono due casi quando si dice una cosa corretta: il primo consiste nel fatto che la si affermi per la semplice ragione che si è molto esperti nell'argomento (e questo rappresenta chiaramente il tuo caso), il secondo è che la si dica poiché si è troppo poco esperti nell'argomento (il mio caso, con estrema certezza).Tarapìa Tapioco ha scritto: ↑6 ott 2023, 23:19 Pertanto, l'equazionenon è corretta alla luce della motivazione da te addotta: una ragione più sottile e profonda si nasconde dietro la possibilità (assolutamente sensata e ragionevole, persino corretta) di riscrivere il termine di derivata della Lagrangiana nella maniera da te svelata.
Il tuo messaggio, ad una prima lettura, mi ha aiutato molto. Non solo hai risposto alla domanda, ma mi hai aiutato a capire anche da dove nascesse il mio dubbio e ciò mi ha portato a ragionare su questioni che non avrei mai potuto affrontare da solo (ad esempio il problema inevitabile di notazione che sorge quando si passa a funzioni a più variabili). Mi riservo del tempo per studiarlo meglio e con più profondità e, dopo aver fatto ciò, porti un'ultima questione che il tuo messaggio ha sollevato in me e che spero mi aiuterai ancora a risolvere. Grazie infinite!
-
Tarapìa Tapioco
- Messaggi: 146
- Iscritto il: 30 lug 2023, 15:28
Re: Relatività ristretta
Sono io a doverti ringraziare per la sostanziosità delle questioni da te poste, veramente impegnative e spinose. Sono pronto a diradare ogni eventuale dubbio. Ho, inoltre, aggiunto una piccola appendice alla Conclusione specifica del mio messaggio precedente, per fissare ancor meglio il punto della situazione.Torros ha scritto: ↑7 ott 2023, 11:07Esistono due casi quando si dice una cosa corretta: il primo consiste nel fatto che la si affermi per la semplice ragione che si è molto esperti nell'argomento (e questo rappresenta chiaramente il tuo caso), il secondo è che la si dica poiché si è troppo poco esperti nell'argomento (il mio caso, con estrema certezza).Tarapìa Tapioco ha scritto: ↑6 ott 2023, 23:19 Pertanto, l'equazionenon è corretta alla luce della motivazione da te addotta: una ragione più sottile e profonda si nasconde dietro la possibilità (assolutamente sensata e ragionevole, persino corretta) di riscrivere il termine di derivata della Lagrangiana nella maniera da te svelata.
Il tuo messaggio, ad una prima lettura, mi ha aiutato molto. Non solo hai risposto alla domanda, ma mi hai aiutato a capire anche da dove nascesse il mio dubbio e ciò mi ha portato a ragionare su questioni che non avrei mai potuto affrontare da solo (ad esempio il problema inevitabile di notazione che sorge quando si passa a funzioni a più variabili). Mi riservo del tempo per studiarlo meglio e con più profondità e, dopo aver fatto ciò, porti un'ultima questione che il tuo messaggio ha sollevato in me e che spero mi aiuterai ancora a risolvere. Grazie infinite!
