SNS 2022/1 tensione superficiale olio-aria

[bosone]

Assumendo di conoscere con grande precisione il valore della tensione superficiale tra l'acqua e l'aria , si vuole misurare la tensione superficiale di un olio vegetale con l'aria attraverso il metodo della goccia pendente da un piccolo tubo. A tal fine vengono effettuate tre prove (A), (B) e (C) con l'acqua di gocce con differenti diametri del tubo che si trovano in condizione di equilibrio meccanico molto vicino alla situazione di distacco dal tubo, mentre la prova (D) riguarda un olio di cui la tensione superficiale con l'aria è ignota allo sperimentatore. Per favorire le estrazioni delle misure da associare, vengono riportate in tabella le lunghezze di due segmenti che indicano rispettivamente il massimo diametro equatoriale della goccia sferica e il diametro della goccia misurato su un piano parallelo al piano equatoriale e posizionato ad una distanza dal piano equatoriale nell'ordine (A)acqua (B)acqua (C)acqua (D) olio

: ; ; ;
: ; ; ;

Le densità dell'acqua e dell'olio a temperatura ambiente sono rispettivamente e . La densità dell'aria vale e l'accelerazione di gravità vale . La forza di gravità e la tensione superficiale sono gli unici elementi che contribuiscono a determinare l'equilibrio e la forma delle gocce.
Determinare il valore della tensione superficiale dell'olio rispetto all'aria fornendo anche una misura dell'incertezza della misura effettuata.

[bosone]

Grazie Pigkappa!

[bosone]

Visto che attualmente nessuno ha raccolto la sfida, provo a postare due hint. La tensione superficiale può riguardarsi o come lavoro necessario ad incrementare dell'unità di area la superficie della goccia o come forza per unità di lunghezza applicata alla circonferenza di raggio al punto di rottura della goccia sollecitato dal peso mg. In questo caso, visti i dati del testo sarà che, introdotte la densità dell'acqua (a) (b) (c) o dell'olio (d) e g, risulta per (a) . Ora per calcolare l'incertezza di occorre calcolare l'incertezza di che è la somma delle incertezze di ottenibile dalla tabella. Quindi per partire basta fare i conti per i tre casi dell'acqua e per il caso dell'olio.....

[Pigkappa]

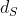
forza per unità di lunghezza applicata alla circonferenza di raggio al punto di rottura della goccia sollecitato dal peso mg

Ti posso chiedere da dove viene questo fatto..? E' un fatto noto? Io della tensione superficiale ricordo poco.

Come individuo che ricorda zero formule della tensione superficiale a parte i concetti base, qui e' quel che avrei iniziato a fare nel test.

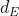
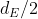
Per ora approssimiamo una goccia come una semisfera attaccata ad un tronco di cono attaccato ad un cilindro. La sfera ha diametro . Ad una altezza sopra al centro della sfera, se sfera fosse intera senza tronco di cono e senza cilindro, dovrebbe avere sezione orizzontale zero. Ma invece a quel punto il cilindro e' cominciato e la sezione ha diametro .

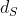
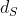
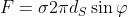
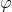
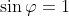
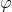
Se consideriamo la circonferenza di diametro , li' direi che agisce una forza di tensione superficiale. Purtroppo si vede da alcune figure che non e' diretta verso l'alto ma inclinata. La componente verso l'alto direi che la stimiamo come dove e' l'angolo con l'orizzontale. E qui o si fa una approssimazione brutale (non troppo giusto nelle figure 1 e 2), oppure si stima dalle figure. Comunque qua secondo me mi sto inventando una formula ispirata alla tua! Ma in realta' la tensione superficiale agisce distribuita su tutta la superficie, e anche se e' vero che ha le dimensioni di forza/lunghezza, non e' cosi' semplice da poter davvero dire che . 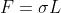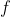Per questo qua piu' in basso introduco un coefficiente che vuole incorporare l'errore che sto facendo. In realta' la cosa corretta, secondo me, sarebbe quella di immaginare di perturbare la goccia, quindi se ne abbassa il baricentro (= la gravita' da' energia) e se ne altera la superficie (=la tensione superficiale assorbe energia) e dall'equilibrio tra queste cose si puo' trovare una condizione... Questo sarebbe complicato ma in realtà forse fattibile, per ora però continuo con questo approccio usando forze e non energie.

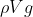
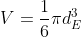
Verso il basso agisce la forza di gravita' dove V e' il volume di liquido sotto quella altezza. Questo volume non e' facile da calcolare, se la goccia fosse una sfera sarebbe , se la si considera una semisfera piu' tronco di cono mi verrebbe (mi sono cercato la formula del volume del tronco di cono ma si puo' anche approssimare in modi piu' facili se serve) . Forse farei una stima grossolana ma specifica per ogni goccia, perche' le forme sono abbastanza diverse.

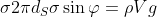
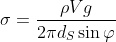
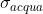
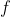
Adesso, dalle formule , stimerei per l'acqua. Verra' che sbaglio di sicuro perche' in questi problemi un fattore geometrico si sbaglia spesso, ma il testo mi ha dato il valore vero di , quindi mi calcolo il fattore di conversione . Quindi correggo la formula sopra: .

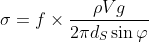
Se dalle 3 gocce d'acqua trovo valori simili di f mi convinco che l'approccio ha senso, altrimenti bisogna ricominciare in modo diverso.

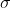
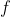
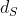
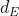
E poi calcolo usando questa formula per l'olio. Le incertezze vengono sia da (ci metterei una bella incertezza sopra, che deriva in parte dalle incertezze delle grandezze misurate per le gocce d'acqua) che da , per l'olio.

[Pigkappa]

Allora, adesso che ho scritto quel che avrei provato a fare qua sopra senza aver cercato questo problema su internet... L'ho cercato su internet. Viene fuori che c'e' un metodo usato per davvero per calcolare la tensione superficiale, chiamato "pendant drop method" in inglese, che per l'appunto usa la forma della goccia.

Da quel che trovo online, non e' che ci sia davvero una formula univoca in funzione di quei diametri messi in evidenza nel testo.

Pero', usando i due parametri , si parametrizza abbastanza bene la forma di una goccia e quindi si possono costruire formule approssimate e abbastanza precise. Una presentazione che ho trovato e' questa.

Sicuramente non e' un problema in cui si deve fare qualcosa di perfetto, ma un problema in cui ci si deve arrangiare e trovare un risultato ragionevole in qualche modo arrabattato.

[bosone]

Io avevo avuto l'idea di calcolare il valor medio di a)b)c) acqua confrontandolo con il valore esatto della tensione dell'acqua e trovare il valore dell'oli confrontandolo con il dato

[Pigkappa]

Sono bloccato, su questo. Usando sia il mio che il tuo metodo si ottengono valori nei casi A, B e C parecchio diversi tra loro. Mi sono inventato un metodo completamente diverso ma anche con quello vengono numeri sbagliati.

Con il mio metodo, ho stimato i volumi stile semisfera piu' tronco di cono; ho stimato dalle figure di 0.90, 0.95, 1.0 nei tre casi A, B e C; ho calcolato e trovo per le tre bolle in N/m i valori 0.027, 0.030, 0.044. Sto sottostimando di un fattore 2 o 3 e soprattutto ottengo valori parecchio diversi tra le tre bolle.

Con il tuo metodo, ottengo 0.090, 0.102, 0.141 che in questo caso sono sovrastimati, un po' meglio dei miei, ma comunque sono parecchio diversi tra loro. Le nostre formule non scalano nel modo corretto in secondo me.

Terzo metodo: per le tre bolle, un po' ad occhio ma neanche troppo, stimo la superficie di tutta la parte che e' sospesa in aria, e il suo volume , e l'altezza del baricentro rispetto all'imboccatura del tubo, e il raggio della sezione del tubo. Mentre si forma la bolla, l'area passa da ad , quindi dall'acqua nella bolla la tensione superficiale assorbe energia . La gravita' fornisce energia . Uguagliando, . Ottengo i tre valori 0.019, 0.014, 0.038 che sono di nuovo sbagliati e parecchio diversi tra loro. Forse sto sbagliando a interpretare il lavoro fatto dalla tensione superficiale.

[bosone]

Non ho potuto rispondere prima mettendo i risultati del metodo usato descritto nel post. Lo farò quanto prima. Anticipo che la risposta alla domanda è per me. Osservo che la tensione olio aria è ufficialmente 0,0319 N/m

[bosone]

La formula della tensione della goccia al punto di rottura con l'aria risulta . L'incertezza x di è la somma delle incertezze di che per esempio nel caso della goccia di acqua a) risulta Fatti i conti risulta in definitiva nel caso a) dell'acqua Con lo stesso procedimento si possono ricavare per le altre due goccie d'acqua b) e c) rispettivamente e . Pertanto è possibile calcolare il valor medio delle tre goccie d'acqua. Esso risulta da a) b) c)
Allora essendo il dato certo viene naturale impostare la seguente relazione essendo x la tensione superficiale richiesta e il dato sperimentale del testo pari a
Fatti i conti risulta in definitiva
(da notare che)

[Pigkappa]

Ok capisco il procedimento, ma il fatto che il valor medio delle 3 misure per l'acqua ti viene fuori dal primo degli intervalli di incertezza è un brutto segno, vuol dire o che il procedimento è sbagliato, o perlomeno che le incertezze sono sottostimate.

Il fatto che bisogna inventarsi questo coefficiente x, che sono d'accordo sia una idea ragionevole e lo avevo menzionato anche io chiamandolo f nel mio post sopra, è però indice del fatto che c'è un'altra fonte di incertezza, cioè il fatto che il nostro metodo non funziona davvero.

Quindi io metterei una incertezza significativamente più alta sul risultato finale.

Comunque ho chiesto a Luca che ha fatto la prova quest'anno e nessuno aveva una soluzione soddisfacente per questo problema. Quel che hai fatto tu sarebbe andato bene.