Esercizio 3 SNS 2022-2023

[Torros]

Non avendo ancora trovato le soluzioni degli esercizi dell'ultimo test, chiedo qui sul forum se qualcuno è riuscito a risolvere l'esercizio sul betatrone. Propongo il risultato che sono riuscito ad ottenere che mi ha soddisfatto di più, ma vi prego di segnalarmi errori (anche perché mi sembra una soluzione troppo semplice ):

Considero la legge di Lenz:

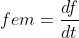
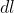
dove f è il flusso del campo magnetico che attraversa la superfice delimitata dall'orbita della particella, generato dall'elettromagnete. La fem è chiaramente pari all'integrale sul ciclo del campo elettrico per e risulta essere uguale al prodotto del campo elettrico per la lunghezza della circonferenza.
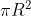
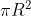
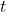
Divido ora entrambi i membri per . Per quanto riguarda il secondo membro posso portare all'interno della derivata, in quanto non dipende da . la funzione da derivare rappresenta ora il valor medio del campo magnetico all'interno della superficie delimitata dalla traiettoria e chiamo tale valore .
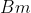
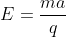
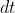
Sostituisco ora al primo membro e porto dal secondo al primo membro per ottenere:

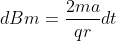
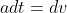
Sostituisco per ottenere:

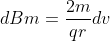
Nulla dipende da v e dunque:

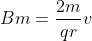
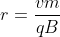
Sostituisco ora ed ottengo che il valor medio del campo magnetico
all'interno della circonferenza vale il doppio del campo magnetico sulla circonferenza.
Che ne pensate? Grazie

[bosone]

Mi pare corretta nel procedimento però si trascura nel conto il - della legge di Faraday per cui i due campi dovrebbero essere opposti (?)

[Torros]

Hai ragione, non lo avevo proprio considerato. Rileggendo la richiesta del testo, tuttavia, mi sono accorto che si chiede di trovare la relazione tra le intensità dei due campi. Con il termine "intensità" dici che si intende il modulo del valore del campo? Grazie ancora.

[bosone]

In effetti per intensità dovrebbe intendersi il valore assoluto del modulo ma in questo caso mi pareva significativo che dovevano risultare opposti. Indaghiamo ancora facendo magari pronunciare Pigkappa....

[Pigkappa]

Vabbè ma almeno postate il testo come fanno gli altri utenti a rispondere?

[bosone]

Si è giusto. Il fatto è che io riporto il testo scritto ma c'è anche lo schema -come una foto- della sezione verticale dell'acceleratore che almeno io non so riportare (rimando per questo al sito SNS).

SNS 2022/3
Un betatrone è un acceleratore in cui particelle di carica q e massa m, che circolano in un tubo a vuoto a forma toroidale, sono mantenute in orbita circolare di raggio fissato R sul piano mediano di un elettromagnete a simmetria cilindrica (ossia con la geometria di un solido di rotazione) e vengono accelerate aumentando nel tempo l'intensità della corrente che genera il campo magnetico e dunque l'intensità del campo stesso. Si assuma che il moto delle particelle sia non relativistico.
Determinare la relazione che ad ogni dato istante deve sussistere tra il valor medio del campo sulla superficie del cerchio racchiuso dall'orbita e l'intensità del campo lungo l'orbita stessa, affinchè sia possibile accelerare le particelle mantenendo costante il raggio dell'orbita.

[Pigkappa]

Scrivo la mia soluzione, e' equivalente a quella di Torros ma provo a fare attenzione ai segni.

Coordinate cilindriche: diretto lungo l'orbita della particella positivo se antiorario, verso l'alto, radiale positivo verso il fuori. Quando indico una variabile e' sempre intesa nel punto dell'orbita, a meno che non ci metta una overline sopra come nel qual caso intendo la media della variabile nel cerchio racchiuso dall'orbita.



E poi:


Quindi:

e derivando .

Mettendo insieme all'equazione trovata sopra, e se entrambi partono da 0, , e quindi secondo me non e' vero che i campi sono opposti, ma hanno la stessa direzione.

[Torros]

Perfetto, mi torna tutto. Ripensandoci è insensato che i due vettori abbiano verso opposto, visto che, in ogni punto appartenente al cerchio che ha per contorno la circonferenza del tubo a vuoto (e in ogni punto appartenente alla circonferenza stessa), il verso del campo è rivolto nello stesso verso del versore . Il campo medio non può dunque che essere rivolto nello stesso verso di , così come il campo sulla circonferenza. Grazie mille Pigkappa per la dimostrazione formale.

[Pigkappa]

Il campo medio sulla superficie del cerchio potrebbe essere di segno opposto al campo sulla linea della circonferenza... La figura che hanno messo nel problema suggerisce che probabilmente non è così, ma si può sicuramente costruire un setup in cui accade.

[bosone]

Credo tuttavia (Torros)che per quanto riguarda la soluzione si possa bypassare questa duplice possibilità dal momento che il testo chiede la relazione fra le INTENSITA' dei campi ovvero fra i valori assoluti dei campi a prescindere appunto dal loro orientamento. Comunque mi fa piacere che la possibilità segnalata da Pigkappa esista.