298. Circuito resistivo.
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
298. Circuito resistivo.
È dato un circuito costituito da sole resistenze, contenuto in una scatola nera, dalla quale fuoriescono quattro terminali  ,
,  ,
, 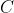 e
e 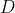 . Sono note le sei resistenze equivalenti
. Sono note le sei resistenze equivalenti 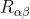 che si ottengono tra i terminali
che si ottengono tra i terminali  e
e 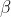 lasciando liberi gli altri due. Si determinino le sei resistenze
lasciando liberi gli altri due. Si determinino le sei resistenze 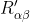 che si ottengono quando invece gli altri due terminali vengono cortocircuitati.
che si ottengono quando invece gli altri due terminali vengono cortocircuitati.
Ultima modifica di Luca Milanese il 8 ago 2022, 12:26, modificato 1 volta in totale.
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
-
DeoGratias
- Messaggi: 150
- Iscritto il: 2 nov 2020, 23:58
- Località: Pisa
Re: 298. Circuito resistivo.
Non ci sono limiti alla crudeltà di un teorico...
Re: 298. Circuito resistivo.
Secondo la mia interpretazione del testo ci sono infatti 6 possibilità di accoppiare i 4 terminali 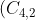 , le combinazioni di 4 oggetti 2 a 2. Per esempio possono essere
, le combinazioni di 4 oggetti 2 a 2. Per esempio possono essere 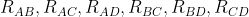 e sono note. Ora sempre secondo me cortocircuitando C e D si hanno le seguenti modifiche
e sono note. Ora sempre secondo me cortocircuitando C e D si hanno le seguenti modifiche
C=D per cui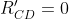
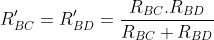 . Analogamente
. Analogamente
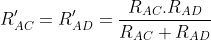 Così, per come ho interpretato io,
Così, per come ho interpretato io, 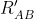 risulta dal parallelo fra
risulta dal parallelo fra 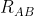 e la somma
e la somma 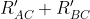
Prima di fare i conti bovini vorrei sapere da te se la via è c ho male interpretato

C=D per cui
Prima di fare i conti bovini vorrei sapere da te se la via è c ho male interpretato
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 298. Circuito resistivo.
Nota anzitutto che 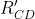 (e analogamente le altre) è definita come la resistenza tra
(e analogamente le altre) è definita come la resistenza tra 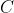 e
e 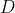 quando
quando  e
e  sono cortocircuitati, non quando lo sono gli stessi
sono cortocircuitati, non quando lo sono gli stessi 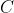 e
e 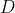 : rischi di fare confusione con la notazione.
: rischi di fare confusione con la notazione.
Dopodiché, i risultati che trovi sono sbagliati: quando tratti le resistenze equivalenti non puoi applicare così semplicemente le usuali leggi di composizioni delle resistenze (se non sei convinto, guarda cosa succede se il circuito nascosto è costituito dal quadrato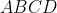 in cui ogni lato ha uguale resistenza). Ti consiglio di cercare un'altra strada.
in cui ogni lato ha uguale resistenza). Ti consiglio di cercare un'altra strada.
Dopodiché, i risultati che trovi sono sbagliati: quando tratti le resistenze equivalenti non puoi applicare così semplicemente le usuali leggi di composizioni delle resistenze (se non sei convinto, guarda cosa succede se il circuito nascosto è costituito dal quadrato
Ultima modifica di Luca Milanese il 12 ago 2022, 17:40, modificato 1 volta in totale.
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 298. Circuito resistivo.
Ho fatto proprio bene a fermarmi perchè pare che non ci abbia capito nulla. Per me le resistenze equivalenti tipo 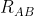 sono quelle che si trovano quando gli altri due terminali sono liberi, come dice il testo. Ora pare che gli altri due debbano essere cortocircuitati...sono proprio confuso, ci ripenserò...
sono quelle che si trovano quando gli altri due terminali sono liberi, come dice il testo. Ora pare che gli altri due debbano essere cortocircuitati...sono proprio confuso, ci ripenserò... 
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 298. Circuito resistivo.
Avevo dimenticato un apostrofo, ora ho corretto. Scusami per l'ulteriore confusione.
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 298. Circuito resistivo.
Ci dai un hint?
Questo non copre necessariamente tutti i circuiti che possono esserci dentro la scatola (o forse si' ma non l'ho dimostrato), ma assumendo che dentro la scatola ogni due punti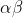 siano connessi solo da un resistore
siano connessi solo da un resistore 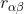 , ho ricavato
, ho ricavato 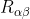 in funzione di tutte le
in funzione di tutte le 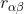 .
.
Se prendo l'espressione di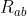 e metto
e metto 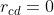 per scrivere
per scrivere 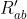 , resta comunque un'espressione relativamente complessa che non riesco a ricondurre alle altre
, resta comunque un'espressione relativamente complessa che non riesco a ricondurre alle altre 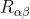 .
.
Ricavare tutte le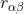 in funzione di
in funzione di 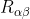 , e poi sostituire nella formula per
, e poi sostituire nella formula per 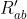 , in teoria e' possibile, ma in pratica mi sembra un conto tremendo. Ci sono molte simmetrie, ma le formule sono abbastanza intrattabili.
, in teoria e' possibile, ma in pratica mi sembra un conto tremendo. Ci sono molte simmetrie, ma le formule sono abbastanza intrattabili.
Questo non copre necessariamente tutti i circuiti che possono esserci dentro la scatola (o forse si' ma non l'ho dimostrato), ma assumendo che dentro la scatola ogni due punti
Se prendo l'espressione di
Ricavare tutte le
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 298. Circuito resistivo.
Passare per le 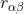 è effettivamente infattibile a livello pratico. Può essere più utile dimostrare preliminarmente che, se inserendo una corrente
è effettivamente infattibile a livello pratico. Può essere più utile dimostrare preliminarmente che, se inserendo una corrente 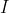 nel nodo
nel nodo  e prelevandola dal nodo
e prelevandola dal nodo 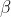 si stabilisce una d.d.p.
si stabilisce una d.d.p. 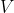 tra i nodi
tra i nodi 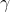 e
e 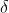 , e se inserendo una corrente
, e se inserendo una corrente 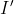 in
in 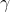 e prelevandola da
e prelevandola da 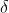 si stabilisce una d.d.p.
si stabilisce una d.d.p. 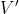 tra
tra  e
e 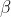 (in due situazioni separate), vale:
(in due situazioni separate), vale:
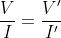
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 298. Circuito resistivo.
Che notazione tremenda mamma mia. Fammi chiamare 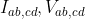 la corrente e la ddp tra i nodi A e B, quando hai inserito una corrente di 1
la corrente e la ddp tra i nodi A e B, quando hai inserito una corrente di 1  in C e la prelevi in D, cosi' che dal nome di una variable si capisce che cosa e'.
in C e la prelevi in D, cosi' che dal nome di una variable si capisce che cosa e'.
Tu dici che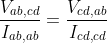 e questo risulta vero dalle mie formule per queste quantita' espresse in funzione di
e questo risulta vero dalle mie formule per queste quantita' espresse in funzione di 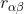 .
.
Ma anche detto questo, non vedo un trucco per risolvere.
Chiamo caso 1 quello iniziale, i dati che abbiamo dal caso 1 sono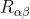 per tutti gli
per tutti gli 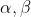 . Chiamo caso 2 quello in cui C e D sono cortocircuitati, vogliamo
. Chiamo caso 2 quello in cui C e D sono cortocircuitati, vogliamo 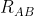 in questo caso. Ho pensato di provare a costruire un caso 3 e usare qualche sovrapposizione in modo che caso 1 + caso 3 = caso 2. In particolare se il circuito del caso 3 e' come quello del caso 1 e inserisco in C ed estraggo in D la corrente
in questo caso. Ho pensato di provare a costruire un caso 3 e usare qualche sovrapposizione in modo che caso 1 + caso 3 = caso 2. In particolare se il circuito del caso 3 e' come quello del caso 1 e inserisco in C ed estraggo in D la corrente 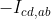 , e sovrappongo al caso 1, mi ritrovo con un circuito in cui non scorre corrente nel ramo tra C e D di resistenza
, e sovrappongo al caso 1, mi ritrovo con un circuito in cui non scorre corrente nel ramo tra C e D di resistenza 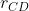 che e' lo stesso che succede nel caso 2. Ma quando mi metto a scrivere correnti e potenziali nel ramo AB per fare la sovrapposizione e vedere se per il caso 2 ottengo una formula che mi si riconduce alla
che e' lo stesso che succede nel caso 2. Ma quando mi metto a scrivere correnti e potenziali nel ramo AB per fare la sovrapposizione e vedere se per il caso 2 ottengo una formula che mi si riconduce alla 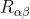 , i conti sono brutti e non mi viene qualcosa che si trasforma come si deve, neanche usando la tua formula sopra.
, i conti sono brutti e non mi viene qualcosa che si trasforma come si deve, neanche usando la tua formula sopra.
Tu dici che
Ma anche detto questo, non vedo un trucco per risolvere.
Chiamo caso 1 quello iniziale, i dati che abbiamo dal caso 1 sono
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
Re: 298. Circuito resistivo.
Domanda a parte... Ma la cosa che dicono qua nella soluzione ("Let us make use of the fact that any "black box" circuit consisting of resistors can be reduced" + figura) ti sembra vera? (A me no)
https://www.sarthaks.com/242316/conceal ... een-clamps
https://www.sarthaks.com/242316/conceal ... een-clamps
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
