296 - Trappola magnetica
Re: 296 - Trappola magnetica
Avevo pensato di considerare termini di 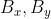 che non uscissero dalla trappola tipo
che non uscissero dalla trappola tipo 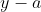 e
e 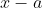 che hanno lo stesso denominatore. Devono essere elevati al quadrato e deve essere estratta la radice. Bisogna trovare il massimo di questa espressione. E' una trada che porta a qualcosa
che hanno lo stesso denominatore. Devono essere elevati al quadrato e deve essere estratta la radice. Bisogna trovare il massimo di questa espressione. E' una trada che porta a qualcosa 

-
DeoGratias
- Messaggi: 150
- Iscritto il: 2 nov 2020, 23:58
- Località: Pisa
Re: 296 - Trappola magnetica
Ti sconsiglio di provare a trovare il massimo analiticamente, visto che probabilmente l'equazione che troveresti non sarebbe neanche risolubile immediatamente (non ho provato, quindi potrei sbagliarmi). Ricordati di considerare anche il campo esterno (non solo quello dei fili), prova a fare un claim sulla direzione ottimale e poi a giustificarlo.
Re: 296 - Trappola magnetica
Il potenziale magnetico dell'atomo dovrebbe essere in generale del tipo 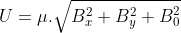 ed il suo massimo dovrebbe risiedere in un punto (x,y,z) verso cui l'atomo dovrebbe dirigersi a partire dall'origine. Ma allora l'atomo dovrebbe uscire dalla trappola che io credevo piana(x,y) penetrando anche lungo l'asse z. E' così o sto prendendo lucciole per lanterne?
ed il suo massimo dovrebbe risiedere in un punto (x,y,z) verso cui l'atomo dovrebbe dirigersi a partire dall'origine. Ma allora l'atomo dovrebbe uscire dalla trappola che io credevo piana(x,y) penetrando anche lungo l'asse z. E' così o sto prendendo lucciole per lanterne? 
Nell'origine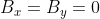 per cui nell'origine
per cui nell'origine 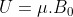 che rimane immutato se l'atomo si sposta sull'asse z e quindi non c'è max. Questo mi porterebbe a dire che nel punto di max sono presenti tutti e tre i campi. Ma non vedo il valore dei primi due che dovrebbero tuttavia essere simmetrici?
che rimane immutato se l'atomo si sposta sull'asse z e quindi non c'è max. Questo mi porterebbe a dire che nel punto di max sono presenti tutti e tre i campi. Ma non vedo il valore dei primi due che dovrebbero tuttavia essere simmetrici? 

Insomma sarebbe possibile avere un hint sulle osservazioni da fare per semplificare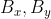 della formula 1 oppure ritieni che ci devo pensare ancora ma non ho altre idee...
della formula 1 oppure ritieni che ci devo pensare ancora ma non ho altre idee... 
Nell'origine
Insomma sarebbe possibile avere un hint sulle osservazioni da fare per semplificare
-
DeoGratias
- Messaggi: 150
- Iscritto il: 2 nov 2020, 23:58
- Località: Pisa
Re: 296 - Trappola magnetica
Lascia stare il movimento lungo l'asse z, la soluzione ottimale è quella in cui l'atomo rimane nel piano 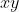 .
.
Prova a pensarla così: più il potenziale in un punto è alto, meno quel punto è "raggiungibile" (servirebbe una maggiore energia cinetica per raggiungerlo). Il potenziale aumenta avvicinandosi a un filo, quindi il tracciato ottimale dovrebbe mantenersi alla stessa distanza tra i due fili tra cui passa.
Prova a pensarla così: più il potenziale in un punto è alto, meno quel punto è "raggiungibile" (servirebbe una maggiore energia cinetica per raggiungerlo). Il potenziale aumenta avvicinandosi a un filo, quindi il tracciato ottimale dovrebbe mantenersi alla stessa distanza tra i due fili tra cui passa.
Re: 296 - Trappola magnetica
2. Allora un percorso opportuno potrebbe essere quello fra i fili 2 e 3 con y=0 e x compreso fra 0 e a. L'espressione di 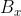 che abbiamo si riduce allora alla somma di quattro frazioni due a due con lo stesso denominatore che può essere scritta agevolmente come
che abbiamo si riduce allora alla somma di quattro frazioni due a due con lo stesso denominatore che può essere scritta agevolmente come = \frac{4\mu_0 a^2 x I}{\pi [a^2+(a+x)^2][a^2+(x-a)^2]}) per cui
per cui
=\frac{16\mu_0^2 a^4 x^2 I^2}{\pi^2[a^2+(x+a)^2]^2[a^2+(x-a)^2]^2}) .
.
Prima di impostare il potenziale si nota che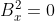 nell'origine e che
nell'origine e che =\frac{16\mu_0^2 I^2}{25\pi^2 a^2}) . Ora si può mostrare che quest'ultimo è il valore massimo assunto nell'intervallo chiuso [0.a]. Infatti considerato
. Ora si può mostrare che quest'ultimo è il valore massimo assunto nell'intervallo chiuso [0.a]. Infatti considerato 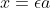 , con
, con  appartenente all'intervallo chiuso [0,1], si ottiene con qualche conto bovino che non ha nulla da invidiare a 1.,
appartenente all'intervallo chiuso [0,1], si ottiene con qualche conto bovino che non ha nulla da invidiare a 1.,=\frac{16 \mu_0^2 \epsilon^2}{\pi^2 a^2(4+\epsilon^4)^2}) Studiandone l'andamento nell'intervallo derivando rispetto a
Studiandone l'andamento nell'intervallo derivando rispetto a  si ottiene il numeratore della derivata
si ottiene il numeratore della derivata \epsilon(8+2\epsilon^4-8\epsilon^3)) che si annulla nell'origine e poi è sempre positivo nell'intervallo dove quindi la funzione è sempre crescente e raggiunge in a il suo massimo.
che si annulla nell'origine e poi è sempre positivo nell'intervallo dove quindi la funzione è sempre crescente e raggiunge in a il suo massimo.
Allora il potenziale agente sull'atomo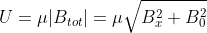 , che vale
, che vale 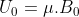 nell'origine, è nel punto di massimo
nell'origine, è nel punto di massimo 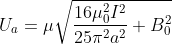 . L'energia cinetica K da conferire all'atomo che seguendo l'asse x arriva in a, deve essere almeno
. L'energia cinetica K da conferire all'atomo che seguendo l'asse x arriva in a, deve essere almeno
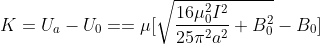
Errori di procedimento e/odi calcolo

Prima di impostare il potenziale si nota che
Allora il potenziale agente sull'atomo
Errori di procedimento e/odi calcolo
-
DeoGratias
- Messaggi: 150
- Iscritto il: 2 nov 2020, 23:58
- Località: Pisa
Re: 296 - Trappola magnetica
Va bene così, vai avanti col prossimo 
Re: 296 - Trappola magnetica
Bene, credo che hai battuto ogni record del forum per quanto riguarda la difficoltà del quesito. Infatti lo hai postato il 26 marzo (!)e sono passati oltre quattro mesi per avere l'accettazione della soluzione da parte tua 


