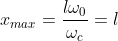Poichè la lunghezza di
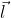
è fissa, si ha:

La velocità di ciascuna carica è allora:
= \dot{\vec R} \pm \frac{\vec \omega \times \vec l}{2})
Perciò la forza agente su ciascuna è:
 \times \vec B \bigg])
La forza totale risulta
 \times \vec B = \frac{\text{d} (q\vec l \times \vec B)}{\text{d}t})
Per la Seconda Legge di Newton:
}{\text{d}t} = \frac{\text{d} (2m \dot{\vec R} ) }{\text{d} t} \Rightarrow \frac{\text{d}}{\text{d}t} \bigg (2m \dot{\vec R} +q\vec B \times \vec l \bigg) = \vec 0 )
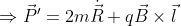
Dall'espressione della forza su ciascuna carica si deduce inoltre che, se inizialmente il dipolo è perpendicolare al campo magnetico, e la sua velocità angolare è ad esso parallela, allora il moto del dipolo si svolgerà sempre in un piano perpendicolare a
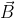
e la sua velocità angolare sarà costante in direzione. Essendo questo il caso del problema, scrivo
)
e
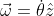
, dove

è l'angolo fra
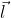
e l'asse delle ascisse. Inoltre scrivo
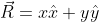
.
Per la conservazione di
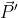
si ha:
}{2m})
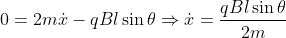
Per la conservazione dell'energia, essendo
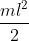
il momento d'inerzia del dipolo attorno a un asse parallelo a
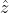
e passante per il suo centro di massa:
)
Si trova così:
}{m^2})
Il dipolo riesce a compiere una rotazione se si ha
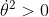
per ogni angolo

:
}{m^2})
Il massimo valore del membro di destra al variare di

è
^2)
, perciò:
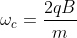
Derivando rispetto al tempo la conservazione dell'energia si ottiene inoltre:
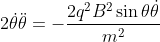
Sostituendo nell'espressione di
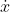
:
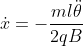
Integrando:
}{2qB}=l \frac{\omega_0 - \dot \theta}{\omega_c})
Perciò la massima distanza lungo

si raggiunge quando
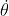
assume il suo minimo valore. Da quanto visto sopra, se
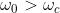
, si ha:
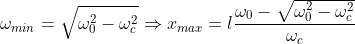
Se
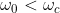
, allora durante la rotazione del dipolo

si annulla e passa a valori negativi, fino al minimo valore
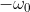
, perciò in questo caso:
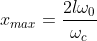
Infine, se
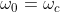
, si ha:
}{2})
Questa equazione differenziale si risolve esplicitamente con la sostituzione
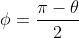
:
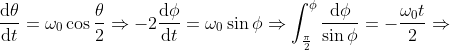
=\pi-4\arctan \bigg (e^{-\frac{\omega_0 t}{2}}\bigg) \Rightarrow \dot \theta(t)=\frac{2\omega_0 e^{-\frac{\omega_0 t}{2}}}{1+e^{-\omega_0 t}} )
Perciò il valore minimo di
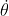
in questo caso è

, che viene raggiunto solo dopo un tempo infinito. Si ha quindi: