Determinare: 1) il tempo t 2) il valore di
266-la goccia si stacca dalla ruota
266-la goccia si stacca dalla ruota
Una ruota di raggio R si muove di puro rotolamento su un terreno bagnato a velocità angolare 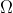 . Ad un certo momento da un punto A, individuato dall'angolo
. Ad un certo momento da un punto A, individuato dall'angolo  che il raggio congiungente A con il centro forma con la verticale, si stacca una goccia d'acqua che cade dopo un certo tempo t esattamente nel punto di contatto che in quell'istante ha la ruota con il terreno.
che il raggio congiungente A con il centro forma con la verticale, si stacca una goccia d'acqua che cade dopo un certo tempo t esattamente nel punto di contatto che in quell'istante ha la ruota con il terreno.
Determinare: 1) il tempo t 2) il valore di in funzione di t
in funzione di t
Determinare: 1) il tempo t 2) il valore di
-
matteofisica
- Messaggi: 70
- Iscritto il: 7 ott 2020, 17:42
Re: 266-la goccia si stacca dalla ruota
Intanto provo a scrivere qualche idea.
La velocità tangenziale del punto A quando la goccia si stacca è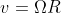 . Da quel momento in poi, la goccia procede di moto parabolico avente equazioni:
. Da quel momento in poi, la goccia procede di moto parabolico avente equazioni:

Detto alpha l'angolo che A forma con la verticale,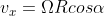 ,
, 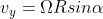 , e
, e ) .
.
Da qui si dovrebbe ricavare t ponendo y=0, ma non so come usare il fatto che la goccia cada esattamente nel punto di contatto ruota-strada.
Forse dovrei invece trovare un'espressione per t dalla prima equazione del sistema?
La velocità tangenziale del punto A quando la goccia si stacca è
Detto alpha l'angolo che A forma con la verticale,
Da qui si dovrebbe ricavare t ponendo y=0, ma non so come usare il fatto che la goccia cada esattamente nel punto di contatto ruota-strada.
Forse dovrei invece trovare un'espressione per t dalla prima equazione del sistema?
Provando e riprovando...
Re: 266-la goccia si stacca dalla ruota
Quello che hai scritto potrebbe andare. Puoi trovare t ma non in funzione di alfa....
-
matteofisica
- Messaggi: 70
- Iscritto il: 7 ott 2020, 17:42
Re: 266-la goccia si stacca dalla ruota
Dunque, possiamo immaginare che, prima del distacco, la goccia si trovasse in cima alla ruota. Se così non è, possiamo comunque traslare verticalmente lo zero dell'energia potenziale di Fp in modo da far quadrare i conti.
Dato che sulla goccia agiscono solo forze conservative, abbiamo che=\frac{1}{2}v^2) .
.
Da qui, sapendo che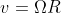 e ricavando alpha, si ottiene
e ricavando alpha, si ottiene ) .
.
E da qui sarei in grado di ricavare t senza aver bisogno di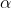 come ho scritto nel post precedente.
come ho scritto nel post precedente.
E' corretto?
Dato che sulla goccia agiscono solo forze conservative, abbiamo che
Da qui, sapendo che
E da qui sarei in grado di ricavare t senza aver bisogno di
E' corretto?
Provando e riprovando...
Re: 266-la goccia si stacca dalla ruota
Sinceramente non posso sapere se è corretto. Per cui se come dici saresti in grado di...finisci il procedimento e trova il risultato! 
-
matteofisica
- Messaggi: 70
- Iscritto il: 7 ott 2020, 17:42
Re: 266-la goccia si stacca dalla ruota
Allora vediamo di concludere:
la distanza orizzontale percorsa dalla goccia nel tempo t è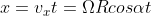 . Affinché sia soddisfatta la condizione che la goccia cada nel punto di appoggio della ruota, la distanza percorsa dalla ruota nello stesso tempo t deve essere
. Affinché sia soddisfatta la condizione che la goccia cada nel punto di appoggio della ruota, la distanza percorsa dalla ruota nello stesso tempo t deve essere 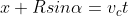 .
.
Dunque, sostituendo e ricordando la condizione di rotolamento puro, si ottiene l'equazione
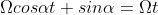
che dà come risultato}) .
.
Dato che, come scritto nel post precedente,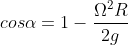 , si ottiene un'espressione per t indipendente dall'angolo alpha:
, si ottiene un'espressione per t indipendente dall'angolo alpha:
^2}}{\frac{\Omega ^3R}{2g}}) , dove nell'ultimo passaggio ho usato l'identità fondamentale
, dove nell'ultimo passaggio ho usato l'identità fondamentale 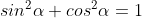 .
.
Se il procedimento è giusto e il risultato è corretto posso passare al secondo punto.
la distanza orizzontale percorsa dalla goccia nel tempo t è
Dunque, sostituendo e ricordando la condizione di rotolamento puro, si ottiene l'equazione
che dà come risultato
Dato che, come scritto nel post precedente,
Se il procedimento è giusto e il risultato è corretto posso passare al secondo punto.
Provando e riprovando...
Re: 266-la goccia si stacca dalla ruota
Il risultato non è corretto così come l'espressione di 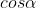 che per certi valori dei parametri potrebbe non essere in valore assoluto minore di 1. Almeno a me risulta infatti incomprensibile questa applicazione della conservazione dell'energia da cui discende il coseno: sembra che l'energia cinetica della goccia uguagli l'energia potenziale. Perchè?
che per certi valori dei parametri potrebbe non essere in valore assoluto minore di 1. Almeno a me risulta infatti incomprensibile questa applicazione della conservazione dell'energia da cui discende il coseno: sembra che l'energia cinetica della goccia uguagli l'energia potenziale. Perchè?
Se vuoi un consiglio sii preciso nel sistema di riferimento cui intendi riferirti. Puoi porre l'origine nello stesso punto A e gli assi uno da sinistra a destra (orizzontale) e uno verso l'alto (verticale). Descrivi il moto della goccia-proiettile come sicuramente sai. Deve passare per il punto di contatto ruota-terreno che, rispetto al riferimento, ha coordinate precise. Puoi determinare ,
, 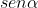 e t. Un metodo più brillante è quello di porsi in un sistema di riferimento in caduta libera con la goccia in cui essa viaggia con la sua velocità uniforme e il terreno si alza verso la goccia con accelerazione g... Si ottiene lo stesso valore di t e di
e t. Un metodo più brillante è quello di porsi in un sistema di riferimento in caduta libera con la goccia in cui essa viaggia con la sua velocità uniforme e il terreno si alza verso la goccia con accelerazione g... Si ottiene lo stesso valore di t e di 

Se vuoi un consiglio sii preciso nel sistema di riferimento cui intendi riferirti. Puoi porre l'origine nello stesso punto A e gli assi uno da sinistra a destra (orizzontale) e uno verso l'alto (verticale). Descrivi il moto della goccia-proiettile come sicuramente sai. Deve passare per il punto di contatto ruota-terreno che, rispetto al riferimento, ha coordinate precise. Puoi determinare
-
matteofisica
- Messaggi: 70
- Iscritto il: 7 ott 2020, 17:42
Re: 266-la goccia si stacca dalla ruota
Allora, pongo l'origine del sistema di riferimento in A come suggerito; l'asse x lo metto nel verso sx-->dx, l'asse y dall'alto verso il basso, in modo da togliere un po' di segni meno. Le equazioni del moto parabolico diventano:

Il punto di contatto ha coordinate=(-Rsin\alpha ,R(1+cos\alpha ))) .
.
Ma adesso mi sorge un dubbio: l'ascissa del punto di contatto non dovrebbe variare nel tempo e corrispondere a quella del centro della ruota, che si muove di moto rettilineo uniforme? Altrimenti come fa la goccia a passare per il punto di contatto muovendosi in avanti lungo l'asse x?
Le coordinate al tempo t non dovrebbero essere=(-Rsin\alpha +\Omega Rt,R(1+cos\alpha )))

Scusami per le domande, ma non mi sento fortissimo in dinamica rotazionale e mi sto impegnando molto per migliorare!
Il punto di contatto ha coordinate
Ma adesso mi sorge un dubbio: l'ascissa del punto di contatto non dovrebbe variare nel tempo e corrispondere a quella del centro della ruota, che si muove di moto rettilineo uniforme? Altrimenti come fa la goccia a passare per il punto di contatto muovendosi in avanti lungo l'asse x?
Le coordinate al tempo t non dovrebbero essere
Scusami per le domande, ma non mi sento fortissimo in dinamica rotazionale e mi sto impegnando molto per migliorare!
Provando e riprovando...
Re: 266-la goccia si stacca dalla ruota
Prima di tutto l'ascissa del punto di contatto mi sembra positiva 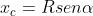 . Poi si ricava il tempo del contatto e.......dovresti trovare tutto. Forse ti dico troppo...
. Poi si ricava il tempo del contatto e.......dovresti trovare tutto. Forse ti dico troppo... 
-
matteofisica
- Messaggi: 70
- Iscritto il: 7 ott 2020, 17:42
Re: 266-la goccia si stacca dalla ruota
Adesso ho capito! Io avevo considerato (sbagliando) che il punto A si trovasse a destra rispetto al centro della ruota e quindi al punto di contatto, mentre esso è a sinistra! Sarei dovuto arrivarci prima...
Comunque sia, riscrivo ancora una volta le formule del moto parabolico e le coordinate del punto di contatto, che, per la condizione di puro rotolamento, è fermo. Il sistema di riferimento è in posizione standard (verso dx e verso l'alto)

\end{matrix}\right.)
Combinando la prima e la terza trovo che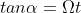 .
.
Ora, conoscendo le identità e
e 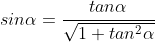 , combinando la seconda e la quarta equazione e operando le sostituzioni
, combinando la seconda e la quarta equazione e operando le sostituzioni  , si arriva ad una equazione di secondo grado in x che ha come unica soluzione accettabile
, si arriva ad una equazione di secondo grado in x che ha come unica soluzione accettabile 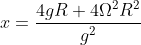 (l'altra è x=0). Da qui, ricordando che
(l'altra è x=0). Da qui, ricordando che 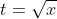 , si giunge alla soluzione:
, si giunge alla soluzione: }) .
.
Comunque sia, riscrivo ancora una volta le formule del moto parabolico e le coordinate del punto di contatto, che, per la condizione di puro rotolamento, è fermo. Il sistema di riferimento è in posizione standard (verso dx e verso l'alto)
Combinando la prima e la terza trovo che
Ora, conoscendo le identità
Provando e riprovando...
