265 - Asta che scivola
-
DeoGratias
- Messaggi: 150
- Iscritto il: 2 nov 2020, 23:58
- Località: Pisa
265 - Asta che scivola
Un'asta omogenea, rigida e sottile di lunghezza 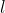 e massa
e massa 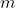 è poggiata verticalmente, in equilibrio instabile, su un piano orizzontale con coefficiente d'attrito
è poggiata verticalmente, in equilibrio instabile, su un piano orizzontale con coefficiente d'attrito 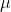 molto elevato (
molto elevato (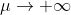 ). Detto
). Detto 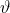 l'angolo che forma con il piano, dopo che all'asta è stata data una spinta infinitesima e ha cominciato a cadere, per un certo
l'angolo che forma con il piano, dopo che all'asta è stata data una spinta infinitesima e ha cominciato a cadere, per un certo 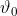 il punto d'appoggio dell'asta comincia a scivolare sul pavimento. Trovare il valore di
il punto d'appoggio dell'asta comincia a scivolare sul pavimento. Trovare il valore di 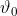
Ultima modifica di DeoGratias il 17 lug 2021, 12:14, modificato 1 volta in totale.
Re: 265 - Asta che scivola
Non posso scrivere LaTeX. Ho provato a considerare le forze di attrito opposte generate da due reazioni normali: quella della componente verticale del moto rotatorio e quella della componente normale della forza centripeta. Quando il loro modulo è uguale l'attrito si annulla qualunque sia mi. Se non ho sbagliato procedimento o calcoli ciò avviene per tetazero uguale ad arcoseno1+radice di 2tutto fratto 3 quando il punto di contatto appunto scivola.
-
DeoGratias
- Messaggi: 150
- Iscritto il: 2 nov 2020, 23:58
- Località: Pisa
Re: 265 - Asta che scivola
@Leo non ho ben capito quali siano le forze che stai considerando, quindi non so dirti di preciso se il procedimento è giusto o no. Il risultato comunque non è corretto, quando puoi prova a ricontrollare i calcoli e a postare il tuo ragionamento 
Re: 265 - Asta che scivola
Ti ringrazio ma non voglio bloccare il gioco per giorni. Chi desidera rispondere lo faccia!! 8 
Re: 265 - Asta che scivola
Il gioco non è bloccato, se qualcuno risolve prima di te ovviamente ti soffia la staffetta
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
Re: 265 - Asta che scivola
Per quello che potrà contare. mi sono accorto stamani che ho messo 3/2 invece di 3/4 e il nuovo valore sarebbe tetazero uguale arcsen (6+radice di 21 tutto fratto 15)...
-
DeoGratias
- Messaggi: 150
- Iscritto il: 2 nov 2020, 23:58
- Località: Pisa
Re: 265 - Asta che scivola
Il risultato ancora non è corretto; prova a considerare il moto che fa l'asta prima di cominciare a scivolare e quali forze sono necessarie per quel moto
Re: 265 - Asta che scivola
Ma ho considerato Ialfa=mg(l/2)costeta e la forza centripeta dedotta dalla conservazione della energia. Poi ho considerato la componente verticale del moto rotatorio e la relativa reazione normale la forza centripeta e la relativa reazione normale. Siccome danno luogo a forze di attrito opposte, imponendo la uguaglianza dei loro moduli si azzera l' attrito qualunque sia il valore di mu.
-
DeoGratias
- Messaggi: 150
- Iscritto il: 2 nov 2020, 23:58
- Località: Pisa
Re: 265 - Asta che scivola
Non capisco bene cosa tu intenda con "due forze d'attrito opposte": come hai detto, puoi usare la conservazione dell'energia, trovare le equazioni del moto e da quelle derivare la forza d'attrito che servirebbe. Prova a risolvere il problema per un qualsiasi valore di 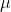 e a pensare in quali condizioni l'asta scivolerebbe, e solo dopo fare il limite con mu che tende a infinito
e a pensare in quali condizioni l'asta scivolerebbe, e solo dopo fare il limite con mu che tende a infinito
Re: 265 - Asta che scivola
Durante la caduta se  è l'angolo formato con l'orizzontale l'equazione di Newton risulta
è l'angolo formato con l'orizzontale l'equazione di Newton risulta cos\theta) dove
dove  è l'accelerazione angolare perpendicolare a (l/2) ed
è l'accelerazione angolare perpendicolare a (l/2) ed 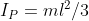 è il momento di inerzia rispetto all'asse per P punto di contatto con il pavimento. Risulta allora
è il momento di inerzia rispetto all'asse per P punto di contatto con il pavimento. Risulta allora(g/l).cos\theta) e l'accelerazione del c.m.
e l'accelerazione del c.m. = -(3/4)g cos\theta) . Istituito un sistema con origine in P asse x orizzontale e asse y verso l'alto, la sua componente verticale sull'asse y è così
. Istituito un sistema con origine in P asse x orizzontale e asse y verso l'alto, la sua componente verticale sull'asse y è così g cos^2\theta) e quella sull'asse x
e quella sull'asse x g cos\theta.sen\theta) . Dalla conservazione dell'energia
. Dalla conservazione dell'energia I_P\omega^2= mg(l/2)(1-sen\theta)) si deduce
si deduce(1-sen\theta)) e la forza centripeta
e la forza centripetamg(1-sen\theta)) che ha componenti sugli assi
che ha componenti sugli assi mg(1-sen\theta)cos\theta , f_{cy}= -(3/2)(1-sen\theta) sen\theta) . Ciò premesso mi risulterebbero le equazioni del moto sostituendo
. Ciò premesso mi risulterebbero le equazioni del moto sostituendo 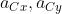
mg cos\theta.sen\theta= -(3/2)mg(1-sen\theta)cos\theta + \mu.N) essendo l'ultima la forza di attrito
essendo l'ultima la forza di attrito
mg cos^2\theta= -mg-(3/2)mg(1-sen\theta)sen\theta + N) essendo N la reazione normale del piano
essendo N la reazione normale del piano
A questo punto, ricavando N dalla seconda e sostituendolo nella prima avevo
mg cos\theta sen\theta + (3/2)mg(1-sen\theta)cos\theta =\mu.[-(3/4)mg cos^2\theta + mg +(3/2)mg(1-sen\theta)sen\theta]) . Pensavo che l'asta sarebbe scivolata se il primo membro fosse stato uguale o maggiore del secondo e, siccome
. Pensavo che l'asta sarebbe scivolata se il primo membro fosse stato uguale o maggiore del secondo e, siccome 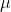 poteva essere comunque grande, il termine fra parentesi quadra si doveva annullare per eliminare l'attrito arrivando così alla determinazione di
poteva essere comunque grande, il termine fra parentesi quadra si doveva annullare per eliminare l'attrito arrivando così alla determinazione di 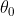 . Ma l'equazione, rifacendo per l'ennesima volta i conti, non ha soluzioni accettabili! Devo aver compiuto errori di procedimento
. Ma l'equazione, rifacendo per l'ennesima volta i conti, non ha soluzioni accettabili! Devo aver compiuto errori di procedimento 

P.S.Mi scuso con te per la pazienza che dovrai avere ma vorrei conoscere i miei errori concettuali.
A questo punto, ricavando N dalla seconda e sostituendolo nella prima avevo
P.S.Mi scuso con te per la pazienza che dovrai avere ma vorrei conoscere i miei errori concettuali.
