Dobbiamo tenere in considerazione il fatto che la q.d.m varia sia sull'asse x (orizzontale) che y (verticale). Prima dell'urto la particella si muove a velocità
261. Semicilindro su un piano
-
DeoGratias
- Messaggi: 150
- Iscritto il: 2 nov 2020, 23:58
- Località: Pisa
Re: 261. Semicilindro su un piano
Provo il 5)
Dobbiamo tenere in considerazione il fatto che la q.d.m varia sia sull'asse x (orizzontale) che y (verticale). Prima dell'urto la particella si muove a velocità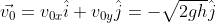 . Dopo l'urto, visto che il semicilindro si muove in avanti con velocità
. Dopo l'urto, visto che il semicilindro si muove in avanti con velocità 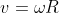 e che contemporaneamente sta ruotando,
e che contemporaneamente sta ruotando, }\hat{i}-\frac{\sqrt{2gh}}{2+\mu(\frac{3}{2}-\frac{8}{3\pi})}\hat{j}) . Se l'urto dura per un tempo
. Se l'urto dura per un tempo 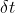 , allora la risultante delle forze sul cilindro sarà
, allora la risultante delle forze sul cilindro sarà }{2+\mu(\frac{3}{2}-\frac{8}{3\pi})}=0) ;
; }=0) , dove
, dove 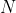 è la reazione vincolare. Ricavando
è la reazione vincolare. Ricavando 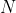 , otteniamo che
, otteniamo che }=kMg\delta t+k\sqrt{2gh}\frac{1+\mu(\frac{3}{2}-\frac{8}{3\pi})}{2+\mu(\frac{3}{2}-\frac{8}{3\pi})}) . Facendo tendere
. Facendo tendere 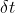 a zero,
a zero, }\approx 0.338)
Dobbiamo tenere in considerazione il fatto che la q.d.m varia sia sull'asse x (orizzontale) che y (verticale). Prima dell'urto la particella si muove a velocità
Re: 261. Semicilindro su un piano
Si', ma mi pare che stai tenendo conto solo della variazione di quantita' di moto della particella, invece secondo me devi considerare quella di tutto il sistema (particella + cilindro).DeoGratias ha scritto: ↑21 giu 2021, 11:03 Dobbiamo tenere in considerazione il fatto che la q.d.m varia sia sull'asse x (orizzontale) che y (verticale).
La variazione di quantita' di moto della particella e' dovuta alla forza impulsiva tra particella e cilindro, che non ci interessa piu' di tanto.
La forza di attrito agisce sul sistema intero (beh, agisce sul cilindro, ma se consideri cilindro+particella come sistema, la forza impulsiva tra i due si cancella perche' e' una forza interna).
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
Re: 261. Semicilindro su un piano
Questa e' la mia soluzione per il 5, se non siete d'accordo ditemi...
Sia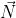 la forza che agisce tra piano e cilindro in O. Siano
la forza che agisce tra piano e cilindro in O. Siano 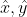 le direzioni orizzontale e verticale. Se non ci fosse attrito
le direzioni orizzontale e verticale. Se non ci fosse attrito 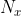 sarebbe 0. Dato che
sarebbe 0. Dato che 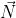 e' l'unica forza esterna agente sul sistema nell'urto (la gravita' e' trascurabile se
e' l'unica forza esterna agente sul sistema nell'urto (la gravita' e' trascurabile se 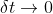 ), l'impulso totale
), l'impulso totale 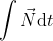 e' uguale alla variazione di quantita' di moto del sistema nell'urto
e' uguale alla variazione di quantita' di moto del sistema nell'urto 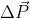 . Possiamo calcolare
. Possiamo calcolare 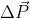 nel caso in cui non ci sia strisciamento perche' abbiamo studiato il moto prima e dopo l'urto nelle domande precedenti.
nel caso in cui non ci sia strisciamento perche' abbiamo studiato il moto prima e dopo l'urto nelle domande precedenti. 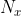 e' dovuta all'attrito per cui, in ogni istante,
e' dovuta all'attrito per cui, in ogni istante, 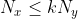 , avendo scelto le direzioni in modo appropriato cosi' che
, avendo scelto le direzioni in modo appropriato cosi' che 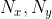 siano positive. Integrando,
siano positive. Integrando, 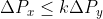 . La forza d'attrito percio' puo' essere sufficiente solo se
. La forza d'attrito percio' puo' essere sufficiente solo se 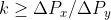
Quantita' di moto del sistema prima dell'urto: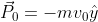 . Dopo l'urto:
. Dopo l'urto: ) \hat x - m w_0 R \hat y) . La differenza e'
. La differenza e' 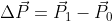 . La condizione limite per evitare strisciamento e':
. La condizione limite per evitare strisciamento e': 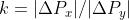 . Facendo i conti e semplificando viene indipendente da
. Facendo i conti e semplificando viene indipendente da 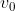 :
:
 \mu}{1 + (\frac{3}{2} - \frac{8}{3\pi}) \mu} = 0.92 )
Se ho contato bene DeoGratias ha risolto 4 domande (compresa la 7 che era impestata) e matteofisica 2, passerei il testimone a DeoGratias ma buon lavoro entrambi
Sia
Quantita' di moto del sistema prima dell'urto:
Se ho contato bene DeoGratias ha risolto 4 domande (compresa la 7 che era impestata) e matteofisica 2, passerei il testimone a DeoGratias ma buon lavoro entrambi
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
-
DeoGratias
- Messaggi: 150
- Iscritto il: 2 nov 2020, 23:58
- Località: Pisa
Re: 261. Semicilindro su un piano
Pigkappa ha scritto: ↑21 giu 2021, 13:01Si', ma mi pare che stai tenendo conto solo della variazione di quantita' di moto della particella, invece secondo me devi considerare quella di tutto il sistema (particella + cilindro).DeoGratias ha scritto: ↑21 giu 2021, 11:03 Dobbiamo tenere in considerazione il fatto che la q.d.m varia sia sull'asse x (orizzontale) che y (verticale).
La variazione di quantita' di moto della particella e' dovuta alla forza impulsiva tra particella e cilindro, che non ci interessa piu' di tanto.
La forza di attrito agisce sul sistema intero (beh, agisce sul cilindro, ma se consideri cilindro+particella come sistema, la forza impulsiva tra i due si cancella perche' e' una forza interna).
Provo a correggere la mia soluzione del 5):
La qdm iniziale della particella è
Per quanto riguarda le forze sul cilindro, sull'asse y si ha
Re: 261. Semicilindro su un piano
Si' e' la stessa soluzione e risultato mio. Io ho evitato di dire cose come "la forza esercitata durante l'urto vale..." perche' sicuramente la forza non e' davvero costante nell'urto, e volevo evitare di parlare di "forza media" a meno che non fosse necessario, ma comunque il risultato e' lo stesso. Vai pure con il 262
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
