257 - Striscia infinita di maglie quadrate
257 - Striscia infinita di maglie quadrate
E' dato un circuito elettrico costituito da una striscia, sequenza infinita di maglie quadrate. Ciascun lato di ogni maglia ha resistenza elettrica R. La striscia inizia con il lato AB posto all'ascissa x=0.
Si determini la resistenza equivalente misurata tra i punti A e B.
Edit: E' la prima parte del problema N. 2 assegnato alla Scuola Universitaria S.Anna di Pisa per l'ammissione al primo anno del Collegio di Ingegneria. www.santannapisa.it>collegio>ingegneria ind. e dell'inf.>ammissione>le prove> fisica 2020-2021
Si determini la resistenza equivalente misurata tra i punti A e B.
Edit: E' la prima parte del problema N. 2 assegnato alla Scuola Universitaria S.Anna di Pisa per l'ammissione al primo anno del Collegio di Ingegneria. www.santannapisa.it>collegio>ingegneria ind. e dell'inf.>ammissione>le prove> fisica 2020-2021
Ultima modifica di Leo il 4 mag 2021, 10:24, modificato 1 volta in totale.
-
DeoGratias
- Messaggi: 150
- Iscritto il: 2 nov 2020, 23:58
- Località: Pisa
Re: 257 - Striscia infinita di maglie quadrate
Per caso torna R) ?
? 

Re: 257 - Striscia infinita di maglie quadrate
Salve, mi chiamo Veronica sono della provincia di Lecce. Vorrei provarci io. Premetto: non sto riuscendo ad usare LaTeX, rimedierò quanto prima.
Dunque, ho provato a immaginare la cosa partenza da destra e “aggiungendo pezzi” man mano. Se considero una prima maglia quadrata, immagino che sia sensato scrivere la resistenza equivalente come}) . Aggiungendo un’altra maglia identica suppongo si avrà
. Aggiungendo un’altra maglia identica suppongo si avrà 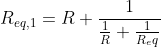 e così via. Quindi aggiungendone all’infinito arriverò a
e così via. Quindi aggiungendone all’infinito arriverò a }}}= R \left( 1+\frac{1}{1+\frac{1}{1+(...)}} \right)=R\phi) , che tende a
, che tende a }{5}) . Scusate la poca formalità
. Scusate la poca formalità 
Dunque, ho provato a immaginare la cosa partenza da destra e “aggiungendo pezzi” man mano. Se considero una prima maglia quadrata, immagino che sia sensato scrivere la resistenza equivalente come
-
DeoGratias
- Messaggi: 150
- Iscritto il: 2 nov 2020, 23:58
- Località: Pisa
Re: 257 - Striscia infinita di maglie quadrate
Anche io avevo fatto un ragionamento simile, immaginando che il circuito sia fatto da  segmenti verticali e poi facendo tendere
segmenti verticali e poi facendo tendere  a infinito. Chiamando
a infinito. Chiamando 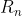 la resistenza sull'
la resistenza sull'  esimo segmento, ho scritto
esimo segmento, ho scritto 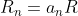 , dove le varie
, dove le varie  sono costanti. Visto che il quadrato finale ha 3 res. in serie, di cui 2 sui segmenti orizzontali pari a
sono costanti. Visto che il quadrato finale ha 3 res. in serie, di cui 2 sui segmenti orizzontali pari a  e una su quello verticale (
e una su quello verticale (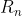 ), avrei che la resistenza equivalente di queste 3 è
), avrei che la resistenza equivalente di queste 3 è }=R(2+a_{n})) . Questa res. è in parallelo a quella sul
. Questa res. è in parallelo a quella sul 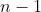 esimo segmento, quindi la resistenza equivalente di queste ultime è pari a
esimo segmento, quindi la resistenza equivalente di queste ultime è pari a ) . Adesso abbiamo quindi un circuito equivalente a quello originario ma con
. Adesso abbiamo quindi un circuito equivalente a quello originario ma con 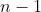 segmenti verticali, dove la resistenza sull'ultimo segmento è
segmenti verticali, dove la resistenza sull'ultimo segmento è 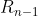 . Ripetendo questa cosa all'infinito, ottengo che
. Ripetendo questa cosa all'infinito, ottengo che R)


Re: 257 - Striscia infinita di maglie quadrate
per VFerzini: ti spieghi bene anche senza latex (te lo dice uno che lo usa da poco con risultati scarsi..). Non capisco perchè è sensato che per un'unica maglia quadrata la R(eq) sia R+1/1/R cioè 2R - semmai dovrebbe essere il parallelo fra R e 3R..
per DeoGratias: ci sono alcune questioni di ragionamento che devi spiegare: 1) che cos'è il segmento verticale ? Perchè a rigore esso ha resistenza R come ogni lato del quadrato. 2) ha senso parlare di ultimo segmento se la struttura è infinita? 3) Perchè il risultato del coefficiente di R è) ? Rispondo con i tuoi
? Rispondo con i tuoi 

per DeoGratias: ci sono alcune questioni di ragionamento che devi spiegare: 1) che cos'è il segmento verticale ? Perchè a rigore esso ha resistenza R come ogni lato del quadrato. 2) ha senso parlare di ultimo segmento se la struttura è infinita? 3) Perchè il risultato del coefficiente di R è
Re: 257 - Striscia infinita di maglie quadrate
Chiedo venia, era un refuso dei miei tentativi di scrivere frazioni in LaTeX finito male e riscritto male, infatti non c’entra palesemente nulla con il resto.  L’eq completa era
L’eq completa era 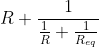 . Questo proprio perché la striscia è infinita e con “ultima maglia” mi sono espressa davvero male a pensarci: non può essere, secondo me, effettivamente tale dato che il circuito è per l’appunto infinito. Sostituendo man mano nell’eq sopra si ottiene quello che prima scrivevo. Non so se mi sono spiegata, si accettano più che volentieri consigli sulla scrittura.
. Questo proprio perché la striscia è infinita e con “ultima maglia” mi sono espressa davvero male a pensarci: non può essere, secondo me, effettivamente tale dato che il circuito è per l’appunto infinito. Sostituendo man mano nell’eq sopra si ottiene quello che prima scrivevo. Non so se mi sono spiegata, si accettano più che volentieri consigli sulla scrittura.
Re: 257 - Striscia infinita di maglie quadrate
Ciao VFersini, benvenuta nel forum. Mi sono permesso di riscrivere i tuoi messaggi precendenti in LaTex in modo che siano più leggibili. Ti consiglio di andare a vedere le modifiche che ho fatto(puoi cliccare su modifica messaggio) per capire come funziona lo strumento.
Sapere aude 
Re: 257 - Striscia infinita di maglie quadrate
Scusa VFersini benvenuta, l'avevo omesso.. Tuttavia non riesco a capire e ti prego di spiegare. La resistenza di una prima maglia quadrata è secondo te 2R. Poi aggiungi un'alra maglia e quella che chiami equazione completa è la serie fra R e il parallelo di R con R(eq), o sbaglio? Questa resistenza a chi è riferita se l'ho capita? a due maglie quadrate? E il risultato poi come fai ottenerlo? Ti prego di essere più esplicita 

 Re: 257 - Striscia infinita di maglie quadrate
Re: 257 - Striscia infinita di maglie quadrate
Allora, cerco di spiegarmi scusate le imprecisioni 
Anzitutto grazie del LaTeX Gamow00, cercherò di imparare a usarlo quanto prima. Dunque. Vediamo un attimo se funziona prendendo direttamente in considerazione direttamente la prima maglia. Facciamo finta di stare guardando il circuito come se fossero le rotaie di un treno, in piedi su AB con il resto davanti. Secondo me la resistenza equivalente in essa può essere considerata come R, cioè la resistenza del cavo stesso, collegata in serie con il parallelo tra l’altra R, il segmento laterale non in comune con altre maglie facciamo a sinistra, e una seconda resistenza equivalente (proprio perché l’ho definita come un a serie tra una resistenza R, in questo caso rappresentata da per es. dal segmento laterale di destra, e una seconda resistenza equivalente, che rappresenta il segmento in comune con la maglia successiva). Per me ha senso dire che il pezzo di cavo in comune con la seconda maglia ha resistenza equivalente uguale ad AB e così via, perché se la striscia è infinita in teoria anche rimuovendo la prima maglia rimarrebbe uguale a sé stessa. Poi il risultato l’ho ottenuto semplicemente raccogliendo R dalla serie infinita. Spero di essere stata chiara
Anzitutto grazie del LaTeX Gamow00, cercherò di imparare a usarlo quanto prima. Dunque. Vediamo un attimo se funziona prendendo direttamente in considerazione direttamente la prima maglia. Facciamo finta di stare guardando il circuito come se fossero le rotaie di un treno, in piedi su AB con il resto davanti. Secondo me la resistenza equivalente in essa può essere considerata come R, cioè la resistenza del cavo stesso, collegata in serie con il parallelo tra l’altra R, il segmento laterale non in comune con altre maglie facciamo a sinistra, e una seconda resistenza equivalente (proprio perché l’ho definita come un a serie tra una resistenza R, in questo caso rappresentata da per es. dal segmento laterale di destra, e una seconda resistenza equivalente, che rappresenta il segmento in comune con la maglia successiva). Per me ha senso dire che il pezzo di cavo in comune con la seconda maglia ha resistenza equivalente uguale ad AB e così via, perché se la striscia è infinita in teoria anche rimuovendo la prima maglia rimarrebbe uguale a sé stessa. Poi il risultato l’ho ottenuto semplicemente raccogliendo R dalla serie infinita. Spero di essere stata chiara
Re: 257 - Striscia infinita di maglie quadrate
Devo essere sincero: ho riflettuto a lungo su quanto hai scritto ma non riesco a dargli un senso. Forse perchè fai un abuso del termine resistenza equivalente. Non ha senso parlare della resistenza equivalente di AB per concludere che è R! LaVFersini ha scritto: ↑24 apr 2021, 20:58 Dunque. Vediamo un attimo se funziona prendendo direttamente in considerazione direttamente la prima maglia. Facciamo finta di stare guardando il circuito come se fossero le rotaie di un treno, in piedi su AB con il resto davanti. Secondo me la resistenza equivalente in essa può essere considerata come R, cioè la resistenza del cavo stesso, collegata in serie con il parallelo tra l’altra R, il segmento laterale non in comune con altre maglie facciamo a sinistra, e una seconda resistenza equivalente (proprio perché l’ho definita come un a serie tra una resistenza R, in questo caso rappresentata da per es. dal segmento laterale di destra, e una seconda resistenza equivalente, che rappresenta il segmento in comune con la maglia successiva).
