257 - Striscia infinita di maglie quadrate
Re: 257 - Striscia infinita di maglie quadrate
Allora ragazzi, mi scuso perché ho avuto modo di riguardare il problema, e mi sono resa conto di aver interpretato male la traccia. L’ho rifatto da capo ed effettivamente la soluzione mi viene uguale a quella di DeoGratias... non so perché avevo interpretato la striscia come infinita da entrambe le parti, e un errore nella considerazione della soluzione mi aveva indotta a pensare che avrei dovuto considerare come parte della stessa Req la resistenza di uno dei due filamenti laterali. Principalmente però avevo capito male il senso dell’infinità del circuito. Scusate tanto, l’ansia fa brutti scherzi 
Re: 257 - Striscia infinita di maglie quadrate
Provando a riflettere sul problema e a risolverlo sono giunto alla stessa conclusione di DeoGratias e con un procedimento affine, tuttavia trovo difficile scrivere una soluzione che sia sufficientemente rigorosa; proverò comunque a dire la mia tenendo conto delle tre domande fatte da Leo.
Considero un circuito analogo a quello del problema, ma con un numero finito di maglie quadrate. Definisco con resistenza verticale qualunque resistenza del circuito geometricamente parallela a quella compresa tra A e B; definisco con resistenza orizzontale qualunque resistenza del circuito geometricamente perpendicolare a quella compresa tra A e B; infine definisco con ultima resistenza verticale l'unica resistenza verticale del circuito (oltre a quella compresa tra A e B) che appartenga ad una e una sola maglia quadrata. L'ultima maglia quadrata del circuito presenta 4 resistenze, due verticali (di cui una è proprio l'ultima resistenza verticale) e due orizzontali: le due orizzontali e l'ultima resistenza verticale sono collegate in serie ed equivalgono ad una resistenza
finito di maglie quadrate. Definisco con resistenza verticale qualunque resistenza del circuito geometricamente parallela a quella compresa tra A e B; definisco con resistenza orizzontale qualunque resistenza del circuito geometricamente perpendicolare a quella compresa tra A e B; infine definisco con ultima resistenza verticale l'unica resistenza verticale del circuito (oltre a quella compresa tra A e B) che appartenga ad una e una sola maglia quadrata. L'ultima maglia quadrata del circuito presenta 4 resistenze, due verticali (di cui una è proprio l'ultima resistenza verticale) e due orizzontali: le due orizzontali e l'ultima resistenza verticale sono collegate in serie ed equivalgono ad una resistenza 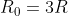 , parallela alla resistenza verticale non considerata. Quest'ultima ed
, parallela alla resistenza verticale non considerata. Quest'ultima ed 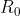 , poichè collegate in parallelo, equivalgono dunque ad una resistenza
, poichè collegate in parallelo, equivalgono dunque ad una resistenza 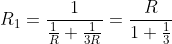 . A questo punto il circuito sarà della stessa tipologia di quello considerato inizialmente, ma con
. A questo punto il circuito sarà della stessa tipologia di quello considerato inizialmente, ma con 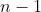 maglie e con l'ultima resistenza verticale di modulo
maglie e con l'ultima resistenza verticale di modulo 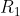 . E' allora possibile ripetere lo stesso procedimento ottenendo un altro circuito che ha l'ultima resistenza verticale di modulo
. E' allora possibile ripetere lo stesso procedimento ottenendo un altro circuito che ha l'ultima resistenza verticale di modulo }}=\frac{R}{1+\frac{1}{2+\frac{1}{1+\frac{1}{3}}) , ed è poi possibile procedere analogamente per le restanti maglie, fino ad ottenere
, ed è poi possibile procedere analogamente per le restanti maglie, fino ad ottenere 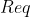 , ossia la resistenza equivalente a quella misurata tra i punti A e B. Nel caso in cui il numero
, ossia la resistenza equivalente a quella misurata tra i punti A e B. Nel caso in cui il numero  di maglie tenda ad infinito non esiste nessuna ultima resistenza verticale e la frazione che esprime
di maglie tenda ad infinito non esiste nessuna ultima resistenza verticale e la frazione che esprime 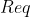 prosegue all'infinito, diventando
prosegue all'infinito, diventando 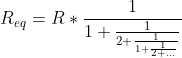 . Per trovare il valore del coefficiente di
. Per trovare il valore del coefficiente di  , pongo
, pongo 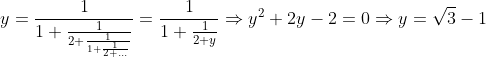
alloraR)
Considero un circuito analogo a quello del problema, ma con un numero
allora
Re: 257 - Striscia infinita di maglie quadrate
Avevo già osservato che il risultato non è congruo e credo che il baco stia proprio nel voler introdurre, anche se iterativamente, l'ULTIMA MAGLIA come aveva fatto DeoGratias. Questo tipo di problemi (vedi SNS 6 del 2011) possono affrontarsi sfruttando la definizione di resistenza cioè, applicando una differenza di potenziale fra A e B e valutando l'intensità di corrente, si ha la resistenza come rapporto fra le due grandezze. Due sono i modi per andare da A a B, o direttamente attraverso R (corrente 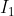 ) o attraverso la striscia infinita (corrente
) o attraverso la striscia infinita (corrente 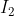 ). Da A partono le due correnti, in B arrivano le due correnti. Basta esaminare le ddp e le correnti nella prima maglia e in entrata nella seconda per accorgersi che non c'è bisogno di allontanarsi dalla PRIMA MAGLIA (il resto della striscia infinita è, come c'era da immaginarsi, assolutamente ridondante). Se vai nel sito citato anche il problema 2, un pò più complicato, si risolve tuttavia nello stesso modo.
). Da A partono le due correnti, in B arrivano le due correnti. Basta esaminare le ddp e le correnti nella prima maglia e in entrata nella seconda per accorgersi che non c'è bisogno di allontanarsi dalla PRIMA MAGLIA (il resto della striscia infinita è, come c'era da immaginarsi, assolutamente ridondante). Se vai nel sito citato anche il problema 2, un pò più complicato, si risolve tuttavia nello stesso modo.
Re: 257 - Striscia infinita di maglie quadrate
Sto continuando a sbattere la testa su questo problema, ma anche tentando di seguire i tuoi hints continua a non tornarmi qualcosa e non riesco a non allontanarmi (perdona la litote) dalla prima delle infinite maglie quadrate.Leo ha scritto: ↑10 mag 2021, 10:28 Avevo già osservato che il risultato non è congruo e credo che il baco stia proprio nel voler introdurre, anche se iterativamente, l'ULTIMA MAGLIA come aveva fatto DeoGratias. Questo tipo di problemi (vedi SNS 6 del 2011) possono affrontarsi sfruttando la definizione di resistenza cioè, applicando una differenza di potenziale fra A e B e valutando l'intensità di corrente, si ha la resistenza come rapporto fra le due grandezze. Due sono i modi per andare da A a B, o direttamente attraverso R (corrente) o attraverso la striscia infinita (corrente
). Da A partono le due correnti, in B arrivano le due correnti. Basta esaminare le ddp e le correnti nella prima maglia e in entrata nella seconda per accorgersi che non c'è bisogno di allontanarsi dalla PRIMA MAGLIA (il resto della striscia infinita è, come c'era da immaginarsi, assolutamente ridondante). Se vai nel sito citato anche il problema 2, un pò più complicato, si risolve tuttavia nello stesso modo.
Seguendo il tuo consiglio ho provato a studiare le varie correnti (chiamando
[P.S.Ho provato anche ad individuare una seconda strada per risolvere il problema, però credo che sia completamente errata visto che mi esce lo stesso risultato trovato in precedenza da DeoGratias e da me (quindi temo di aver reintrodotto indirettamente il concetto di "ultima maglia" o qualche altra fesseria); proverò a presentarla lo stesso perché nel caso in cui fosse sbagliata non riesco a capire dove sia l'errore.
Re: 257 - Striscia infinita di maglie quadrate
Cerco di riprendere dal tuo PS perchè non hai avuto fede nel suggerimento. Seguo i tuoi vertici in senso antiorario ABCD. Da A partono 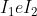 e in B esse arrivano. Su questo non ci sono dubbi. Allora
e in B esse arrivano. Su questo non ci sono dubbi. Allora 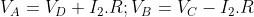 per cui, sottraendo,
per cui, sottraendo, + 2I_2.R) . Ma è anche
. Ma è anche 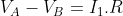 per cui
per cui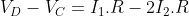 . Se dividi per R scopri allora che la corrente che va da D a C è
. Se dividi per R scopri allora che la corrente che va da D a C è 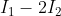 . Se ci riferiamo al nodo D si vede allora che la corrente che dovrebbe entrare nella seconda maglia è
. Se ci riferiamo al nodo D si vede allora che la corrente che dovrebbe entrare nella seconda maglia è 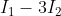 che si annullerebbe, cioè nessuna corrente proseguirebbe nella seconda maglia, se
che si annullerebbe, cioè nessuna corrente proseguirebbe nella seconda maglia, se I_1) Ebbene questo è il nostro caso reale della prima maglia in cui .....per cui la R(eq) è....Se lo finisci ti sei meritato il testimone
Ebbene questo è il nostro caso reale della prima maglia in cui .....per cui la R(eq) è....Se lo finisci ti sei meritato il testimone 

Re: 257 - Striscia infinita di maglie quadrate
Fino a qua mi è tutto chiaro, si tratta della stessa conclusione a cui sono pervenuto durante il mio tentativo di risoluzione imponendo la conservazione dell'energia con la legge dei nodiLeo ha scritto: ↑13 mag 2021, 16:56 Cerco di riprendere dal tuo PS perchè non hai avuto fede nel suggerimento. Seguo i tuoi vertici in senso antiorario ABCD. Da A partonoe in B esse arrivano. Su questo non ci sono dubbi. Allora
per cui, sottraendo,
. Ma è anche
per cui
. Se dividi per R scopri allora che la corrente che va da D a C è
.
Questo è ciò che mi sfugge: per la prima legge di Kirchhoff
Provando inoltre a verificare per quale valore di
Qua non ho capito cosa intendi con "caso reale"
Chiedo ancora scusa nel caso in cui abbia detto altre sciocchezze; mi sa che in 'sti giorni andrò a riguardarmi per bene elettromagnetismo e circuiti perché sono un po' arrugginito
Re: 257 - Striscia infinita di maglie quadrate
Io non so come esprimermi meglio e tu hai dato il risultato giusto per R(eq)= (3/4)R. Quindi per me può bastare e il testimone è tuo  . Giudico inutile l'investigazione successiva visto che nel nostro caso reale (lo ribadisco)
. Giudico inutile l'investigazione successiva visto che nel nostro caso reale (lo ribadisco)I_1) e nemmeno un elettrone entra nella seconda maglia. Quindi nessun elettrone entra nel resto della striscia infinita che pertanto si riduce alla sola prima maglia!! P.S. Ribadisco il consiglio di andare nel sito citato e fare anche il problema 2 che non ho riportato perchè il circuito è complicato e bisogna vederlo.
e nemmeno un elettrone entra nella seconda maglia. Quindi nessun elettrone entra nel resto della striscia infinita che pertanto si riduce alla sola prima maglia!! P.S. Ribadisco il consiglio di andare nel sito citato e fare anche il problema 2 che non ho riportato perchè il circuito è complicato e bisogna vederlo.
Re: 257 - Striscia infinita di maglie quadrate
Perdona la mia ottusità, ma ti porrò un'ultima domanda, sta volta strettamente teorica (ti giuro che è l'ultima, poi non ti tedierò più  ): il fatto che la corrente non passa nella seconda maglia è dovuto al fatto che il circuito è infinito, giusto? Perché se considero un circuito analogo, ma con un numero
): il fatto che la corrente non passa nella seconda maglia è dovuto al fatto che il circuito è infinito, giusto? Perché se considero un circuito analogo, ma con un numero  finito di maglie, la resistenza equivalente tra A e B varia a seconda di
finito di maglie, la resistenza equivalente tra A e B varia a seconda di  (ad esempio la
(ad esempio la 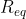 tra A e B in un circuito a una maglia è leggermente inferiore rispetto alla
tra A e B in un circuito a una maglia è leggermente inferiore rispetto alla 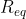 di un circuito a due maglie) e la corrente che passa per le maglie successive la prima univocamente definita da
di un circuito a due maglie) e la corrente che passa per le maglie successive la prima univocamente definita da 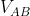 e da
e da  , e risulta perciò impossibile impedire che la corrente passi per la seconda/terza/... maglia
, e risulta perciò impossibile impedire che la corrente passi per la seconda/terza/... maglia
P.S. preferirei lasciare il testimone a te/qualcuno che abbia da proporre problemi ben più interessanti di quelli da me conosciuti (perlopiù provenienti dall'Halliday o da questo sito e perciò già risolti)
P.S. preferirei lasciare il testimone a te/qualcuno che abbia da proporre problemi ben più interessanti di quelli da me conosciuti (perlopiù provenienti dall'Halliday o da questo sito e perciò già risolti)
Re: 257 - Striscia infinita di maglie quadrate
Non credo che sia dovuto al fatto che è infinito ma al fatto che nella prima maglia I_1) . Infatti si conclude che tutta la infinita striscia equivale alla PRIMA MAGLIA. Dalla seconda in poi è come se non ci fosse e si potrebbe tagliare.
. Infatti si conclude che tutta la infinita striscia equivale alla PRIMA MAGLIA. Dalla seconda in poi è come se non ci fosse e si potrebbe tagliare.
Quanto al testimone della staffetta, posi anche io lo stesso problema e altri hanno fatto lo stesso, compreso anche te ora. Ma gli utenti esperti, punti di riferimento del forum, fecero giustamente osservare che bisogna pur cominciare. Se vogliamo dirla tutta, escludendo gli esperti, c'è solo un fuoriclasse; noi siamo tutti equivalenti. Questo io l'ho preso dal S.Anna e altri da SNS... Quindi forza e goditi questa tua prima volta con il 258!!

Quanto al testimone della staffetta, posi anche io lo stesso problema e altri hanno fatto lo stesso, compreso anche te ora. Ma gli utenti esperti, punti di riferimento del forum, fecero giustamente osservare che bisogna pur cominciare. Se vogliamo dirla tutta, escludendo gli esperti, c'è solo un fuoriclasse; noi siamo tutti equivalenti. Questo io l'ho preso dal S.Anna e altri da SNS... Quindi forza e goditi questa tua prima volta con il 258!!
