256. Quadrato che striscia e ruota.
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
256. Quadrato che striscia e ruota.
Una lamina quadrata di vertici  ,
,  ,
, 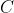 e
e 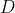 , perfettamente liscia, si muove su un piano orizzontale senza attrito. Sia
, perfettamente liscia, si muove su un piano orizzontale senza attrito. Sia 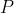 il punto medio del lato
il punto medio del lato 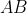 . A un certo istante si osserva che le velocità di
. A un certo istante si osserva che le velocità di  e
e  sono perpendicolari fra loro, mentre la velocità del vertice
sono perpendicolari fra loro, mentre la velocità del vertice 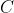 ha modulo
ha modulo  e forma col lato
e forma col lato 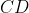 un angolo la cui tangente è
un angolo la cui tangente è  . Si determinino i possibili moduli della velocità di
. Si determinino i possibili moduli della velocità di 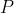 nello stesso istante.
nello stesso istante.
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 256. Quadrato che striscia e ruota.
Poi butterò giù anche il procedimento analitico. Intanto volevo sapere. Per determinare la traccia sul quadrato dell'asse istantaneo di rotazione si trova il punto di incontro di almeno due perpendicolari alle velocità di due punti per esempio B e C. La perpendicolare alla velocità di C spiccata da C passa secondo me per P e dunque il centro di rotazione istantanea si trova su PC. Ho trovato una soluzione in cui , se O è questo centro, (l/2)) . In questo caso passa per O anche la perpendicolare a
. In questo caso passa per O anche la perpendicolare a 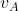 . Ma non è sempre così. Il mio è un approccio ragionevole o è tutto sballato??
. Ma non è sempre così. Il mio è un approccio ragionevole o è tutto sballato?? 
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 256. Quadrato che striscia e ruota.
Se con 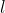 stai indicando il lato del quadrato, ciò che dici è corretto e il tuo approccio mi pare sensato.
stai indicando il lato del quadrato, ciò che dici è corretto e il tuo approccio mi pare sensato. 
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 256. Quadrato che striscia e ruota.
Allora,tanto per concludere su questo punto, si trova facilmente che .\sqrt 5) mentre PO=(l/2) e quindi
mentre PO=(l/2) e quindi (\sqrt 5 - 1)) . In definitiva allora la soluzione sarebbe
. In definitiva allora la soluzione sarebbe .(\sqrt 5+1)) . Siccome chiedi i possibili moduli, immagino di dover cercare come stavo facendo altre possibilità.
. Siccome chiedi i possibili moduli, immagino di dover cercare come stavo facendo altre possibilità. 

-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 256. Quadrato che striscia e ruota.
Infatti c'è anche un altro valore: pensa se il punto 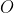 che hai trovato è l'unico possibile...
che hai trovato è l'unico possibile...
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 256. Quadrato che striscia e ruota.
Si, si infatti avevo trovato anche O', simmetrico di O rispetto a P e giacente sulla stessa CP però fuori dal quadrato. In questo caso mi risultava (\sqrt 5+1)) e quindi
e quindi .(l/2)=(v/4)(\sqrt 5-1)) . Il centro istantaneo fuori dal quadrato mi ha sorpreso. Allora ho fatto una ricerca supponendo che v entrasse dentro il quadrato formando ovviamente lo stesso angolo con CD ed essendo la perpendicolare a v tutta esterna al quadrato. Dopo un'ora (duro eh...) mi è sembrato di aver capito che non ci fossero altre soluzioni. Anche tu parli di un altro valore...
. Il centro istantaneo fuori dal quadrato mi ha sorpreso. Allora ho fatto una ricerca supponendo che v entrasse dentro il quadrato formando ovviamente lo stesso angolo con CD ed essendo la perpendicolare a v tutta esterna al quadrato. Dopo un'ora (duro eh...) mi è sembrato di aver capito che non ci fossero altre soluzioni. Anche tu parli di un altro valore... 
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 256. Quadrato che striscia e ruota.
Corretto! I due valori che hai trovato sono quelli che volevo.
La staffetta è tua, ma magari prima di postare il 257 scrivi per bene il procedimento di questo problema a beneficio degli altri utenti.
La staffetta è tua, ma magari prima di postare il 257 scrivi per bene il procedimento di questo problema a beneficio degli altri utenti.
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 256. Quadrato che striscia e ruota.
Il moto del quadrato è rotatorio e si tratta di trovare il centro istantaneo di rotazione traccia dell'asse di rotazione perpendicolare perpendicolare al piano del quadrato. Per determinare il centro si deve trovare l'intersezione delle perpendicolari alle velocità di due punti. Intanto la perpendicolare alla 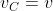 forma con BC lo stesso angolo che v forma con CD a tangente 1/2. Pertanto è facile osservare che essa attraversa il quadrato e passa per P. Infatti
forma con BC lo stesso angolo che v forma con CD a tangente 1/2. Pertanto è facile osservare che essa attraversa il quadrato e passa per P. Infatti =(l/2)=BP) Inoltre si ricava facilmente
Inoltre si ricava facilmente \sqrt 5) . Il centro o i centri istantanei di rotazione stanno su questa retta. Considerati allora A e B che hanno velocità perpendicolari hanno anche le perpendicolari a queste velocità perpendicolari, anche se si considerano le loro opposte. Dunque viene a formarsi il rettangolo AOBO', con O e O' possibili centri istantanei di rotazione . Il rettangolo ha diagonale AB e P punto medio dista allora (l/2) sia da O che da O' uno dentro e uno fuori dal quadrato. Si vede allora che nel caso di O abbiamo
. Il centro o i centri istantanei di rotazione stanno su questa retta. Considerati allora A e B che hanno velocità perpendicolari hanno anche le perpendicolari a queste velocità perpendicolari, anche se si considerano le loro opposte. Dunque viene a formarsi il rettangolo AOBO', con O e O' possibili centri istantanei di rotazione . Il rettangolo ha diagonale AB e P punto medio dista allora (l/2) sia da O che da O' uno dentro e uno fuori dal quadrato. Si vede allora che nel caso di O abbiamo\sqrt 5 - (l/2)=(l/2)(\sqrt 5 -1) ) . Essendo il rapporto ( v/CO) la velocità angolare risulta
. Essendo il rapporto ( v/CO) la velocità angolare risulta . ( l/2) = (v/4)(\sqrt 5 +1)) mentre nel caso di O' il rapporto (v/CO') è minore e risulta
mentre nel caso di O' il rapporto (v/CO') è minore e risulta (\sqrt 5 -1))
