Determinare: 1) le densità superficiali di carica e le densità superficiali di polarizzazione 2) Se
255- Condensatore sferico
255- Condensatore sferico
Si considerino due sfere metalliche spesse concentriche: la sfera interna ha raggi 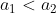 e quella esterna
e quella esterna 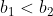 . Lo spazio fra le due sfere è riempito con materiale dielettrico isolante di costante
. Lo spazio fra le due sfere è riempito con materiale dielettrico isolante di costante 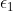 . Una carica
. Una carica 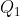 è depositata sulla sfera interna ed una carica
è depositata sulla sfera interna ed una carica 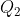 su quella esterna.
su quella esterna.
Determinare: 1) le densità superficiali di carica e le densità superficiali di polarizzazione 2) Se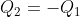 , la capacità del condensatore.
, la capacità del condensatore.
Determinare: 1) le densità superficiali di carica e le densità superficiali di polarizzazione 2) Se
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 255- Condensatore sferico
Definisco le densità di carica superficiale libera 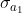 ,
, 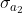 ,
, 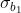 ,
, 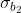 con ovvio significato. Inoltre siano
con ovvio significato. Inoltre siano 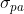 e
e 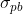 le densità di carica di polarizzazione sulle superfici di raggi
le densità di carica di polarizzazione sulle superfici di raggi 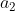 e
e 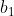 .
.
La carica totale libera sulla sfera interna è) , e similmente
, e similmente ) . Per il Teorema di Gauss, il campo elettrico tra i raggi
. Per il Teorema di Gauss, il campo elettrico tra i raggi 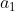 e
e 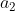 vale
vale 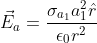 ; allo stesso modo, fra i raggi
; allo stesso modo, fra i raggi 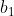 e
e 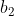 , esso vale
, esso vale 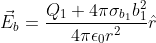 . Tuttavia, essendo le due sfere metalliche, esse sono conduttrici, e quindi al loro interno, se si è in condizioni di elettrostatica, il campo elettrico è nullo:
. Tuttavia, essendo le due sfere metalliche, esse sono conduttrici, e quindi al loro interno, se si è in condizioni di elettrostatica, il campo elettrico è nullo:
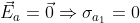
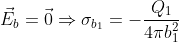
Da ciò, con le equazioni di sopra, si ricavano anche:
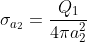

Tra i raggi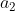 e
e 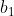 , dove è presente il materiale dielettrico, il campo elettrico vale
, dove è presente il materiale dielettrico, il campo elettrico vale 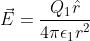 . La polarizzazione vale
. La polarizzazione vale 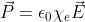 , essendo
, essendo 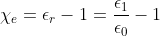 , perciò
, perciò =\frac{Q_1(\epsilon_1-\epsilon_0)\hat r}{4 \pi \epsilon_1 r^2}) . La densità di carica superficiale di polarizzazione si ottiene come
. La densità di carica superficiale di polarizzazione si ottiene come 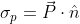 , essendo
, essendo 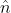 il versore normale alla superficie.
il versore normale alla superficie.
A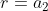 si ha
si ha 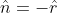 , quindi
, quindi  \cdot \hat r = \frac{Q_1(\epsilon_0-\epsilon_1)}{4\pi \epsilon_1 a_2^2}) .
.
A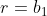 invece è
invece è  e quindi
e quindi }{4\pi b_1^2 \epsilon_1})
Infine, la differenza di potenziale fra i due gusci si ottiene come:
}{4 \pi \epsilon_1 a_2 b_1}) .
.
Per definizione si ha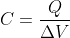 , quindi
, quindi 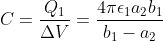
La carica totale libera sulla sfera interna è
Da ciò, con le equazioni di sopra, si ricavano anche:
Tra i raggi
A
A
Infine, la differenza di potenziale fra i due gusci si ottiene come:
Per definizione si ha
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 255- Condensatore sferico
Mah, direi che i risultati sono corretti e che il procedimento è inappuntabile. Vai pure con il prossimo che sarà ben più complicato ! 


