252 - Sfera con buco
-
DeoGratias
- Messaggi: 150
- Iscritto il: 2 nov 2020, 23:58
- Località: Pisa
252 - Sfera con buco
In una regione sferica di raggio  è presente una carica per unità di volume uniforme
è presente una carica per unità di volume uniforme 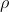 . Viene ricavata una cavità sferica di raggio
. Viene ricavata una cavità sferica di raggio 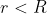 al suo interno. Dimostrare che il campo elettrico in tutti i punti della cavità è uniforme ed è dato da
al suo interno. Dimostrare che il campo elettrico in tutti i punti della cavità è uniforme ed è dato da 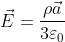 , dove
, dove 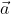 è il vettore posizione diretto dal centro della sfera al centro della cavità.
è il vettore posizione diretto dal centro della sfera al centro della cavità.
-
Ein Bonner
- Messaggi: 6
- Iscritto il: 13 feb 2021, 18:45
Re: 252 - Sfera con buco
Il campo elettrico e' dato dalla somma di un campo elettrico generato dalla sfera grande piu il campo generato dalla sfera piccola, ma con carica opposta.
Consideriamo un sistema di riferimento con centro nella sfera grande:
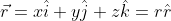
Usiamo il teorema di Gauss per la sfera grande, il cui volume e'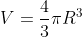 . Inoltre
. Inoltre 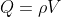 . Abbiamo
. Abbiamo

La simmetria del problema ci dice che E e' radiale, quindi lo possiamo portare fuori dall'integrale e
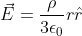
Se facciamo lo stesso gioco conla sfera piccola abbiamo
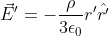
dove la coordinata primata e' centrata nella sfera piccola.
Questi vettori posizione hanno la proprieta
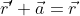
Usando questo fatto, la somma dei campi elettrici, ovvero il campo nella cavita, e
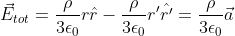
Consideriamo un sistema di riferimento con centro nella sfera grande:
Usiamo il teorema di Gauss per la sfera grande, il cui volume e'
La simmetria del problema ci dice che E e' radiale, quindi lo possiamo portare fuori dall'integrale e
Se facciamo lo stesso gioco conla sfera piccola abbiamo
dove la coordinata primata e' centrata nella sfera piccola.
Questi vettori posizione hanno la proprieta
Usando questo fatto, la somma dei campi elettrici, ovvero il campo nella cavita, e
-
matteofisica
- Messaggi: 70
- Iscritto il: 7 ott 2020, 17:42
Re: 252 - Sfera con buco
Provo a risolverlo!
Allora, per risolvere il problema possiamo usare il principio di sovrapposizione, ossia per trovare il campo elettrico nella cavità togliamo dal campo elettrico all'interno della sfera (ad una distanza a dal centro) quello all'interno del guscio sferico - che in realtà è 0.
Il campo elettrico in una sfera è dato da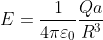
Possiamo esprimere Q come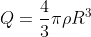
Pertanto, sostituendo nella prima equazione scritta e semplificando un po' le frazioni, si ottiene la tesi.
Una dimostrazione - seppur qualitativa - del fatto che il campo è uniforme, potrebbe essere data dal fatto che una carica di prova posta nella cavità sia attratta da tutte le direzioni e che la somma dei vettori sia sempre costante (che è la stessa cosa che accade nel caso gravitazionale se ci troviamo all'interno di un corpo celeste).
Spero di aver detto tutto giusto e non esitate a correggermi se ho preso qualche granchio!
Allora, per risolvere il problema possiamo usare il principio di sovrapposizione, ossia per trovare il campo elettrico nella cavità togliamo dal campo elettrico all'interno della sfera (ad una distanza a dal centro) quello all'interno del guscio sferico - che in realtà è 0.
Il campo elettrico in una sfera è dato da
Possiamo esprimere Q come
Pertanto, sostituendo nella prima equazione scritta e semplificando un po' le frazioni, si ottiene la tesi.
Una dimostrazione - seppur qualitativa - del fatto che il campo è uniforme, potrebbe essere data dal fatto che una carica di prova posta nella cavità sia attratta da tutte le direzioni e che la somma dei vettori sia sempre costante (che è la stessa cosa che accade nel caso gravitazionale se ci troviamo all'interno di un corpo celeste).
Spero di aver detto tutto giusto e non esitate a correggermi se ho preso qualche granchio!
Provando e riprovando...
-
matteofisica
- Messaggi: 70
- Iscritto il: 7 ott 2020, 17:42
Re: 252 - Sfera con buco
Scusate! Non mi ero accorto che mentre rispondevo era già stata data la risposta! 
Mi sembrava che la mia fosse troppo scontata!
Mi sembrava che la mia fosse troppo scontata!
Provando e riprovando...
-
DeoGratias
- Messaggi: 150
- Iscritto il: 2 nov 2020, 23:58
- Località: Pisa
Re: 252 - Sfera con buco
@Ein Bonner tutto perfetto, vai pure col 253! 
@matteofisica nessun problema, vedrai che ti potrai rifare con i prossimi!
@matteofisica nessun problema, vedrai che ti potrai rifare con i prossimi!
