250. Cariche, sbarretta e campo magnetico.
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 250. Cariche, sbarretta e campo magnetico.
Quando vedi un pezzo di LaTeX criptato, prova a ricaricare la pagina finché non si legge. Quanto alla componente di 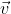 fuori dal piano, a te non interessa, poiché come stavi giustamente facendo devi solo considerare la componente
fuori dal piano, a te non interessa, poiché come stavi giustamente facendo devi solo considerare la componente  dell'equazione.
dell'equazione.
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 250. Cariche, sbarretta e campo magnetico.
Dopo aver spedito ho letto anche il tuo ultimo post. Ma perchè allora 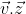 non vale
non vale 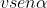 ? Sono confuso e causa dad riprenderò nel pomeriggio. Non so come ringraziarti se puoi indirizzarmi ancora....
? Sono confuso e causa dad riprenderò nel pomeriggio. Non so come ringraziarti se puoi indirizzarmi ancora....
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 250. Cariche, sbarretta e campo magnetico.
Distinguiamo tre componenti tra loro perpendicolari di 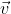 : la componente giaciente nel piano di sbarretta e asse delle
: la componente giaciente nel piano di sbarretta e asse delle  , parallela all'asse delle
, parallela all'asse delle  ; la componente giacente in questo stesso piano ma perpendicolare all'asse
; la componente giacente in questo stesso piano ma perpendicolare all'asse  ; la componente perpendicolare al piano definito. Se le chiamiamo
; la componente perpendicolare al piano definito. Se le chiamiamo 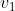 ,
, 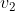 e
e  , abbiamo
, abbiamo 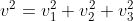 . Inoltre, per definizione, risulta
. Inoltre, per definizione, risulta 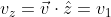 . Tuttavia, e dovrebbe essere chiaro facendo un disegno, in generale non vale
. Tuttavia, e dovrebbe essere chiaro facendo un disegno, in generale non vale 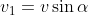 , bensì
, bensì 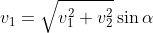 . Ciò significa che che devi trovare un altro modo per esprimere
. Ciò significa che che devi trovare un altro modo per esprimere  , e ti consigliavo di usarne la definizione
, e ti consigliavo di usarne la definizione  .
.
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 250. Cariche, sbarretta e campo magnetico.
Se ho fatto bene la figura otterrei = R cos \alpha(t)) da cui
da cui = - R sen\alpha.(d\alpha/dt)) e dunque
e dunque = - \frac{\sqrt{v_1^2+v_2^2}}{R}) . E' possibile? Se fosse giusto dovrei ricavare in funzione di v e integrare? O cosa?
. E' possibile? Se fosse giusto dovrei ricavare in funzione di v e integrare? O cosa? 

-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 250. Cariche, sbarretta e campo magnetico.
Lascia perdere 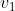 e
e 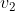 , le avevo introdotte solo per chiarirti il punto degli ultimi messaggi. Hai trovato giustamente
, le avevo introdotte solo per chiarirti il punto degli ultimi messaggi. Hai trovato giustamente 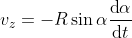 , e sai pure che
, e sai pure che 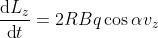 : ormai ti manca pochissimo...
: ormai ti manca pochissimo...
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 250. Cariche, sbarretta e campo magnetico.
La tua infinita pazienza sopporterà le mie due fissazioni da ieri. 1) il vettore 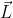 dovrebbe essere sempre perpendicolare a z e dunque
dovrebbe essere sempre perpendicolare a z e dunque 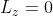 ? 2) Perchè poi con quell'integrale in
? 2) Perchè poi con quell'integrale in 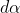 (integrato fra
(integrato fra 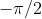 e
e 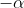 ?) dovrei trovare il valor MINIMO di
?) dovrei trovare il valor MINIMO di  ? Fra l'altro il suo valore relativo mi verrebbe
? Fra l'altro il suo valore relativo mi verrebbe 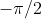 e in assoluto mi verrebbe 0
e in assoluto mi verrebbe 0 



-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 250. Cariche, sbarretta e campo magnetico.
Immagina (e disegna) la sbarretta e le velocità delle cariche nel momento in cui si è raggiunto l'angolo minimo: ciò dovrebbe rispondere alle tue domande e permetterti di completare.
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 250. Cariche, sbarretta e campo magnetico.
Io immagino che inizialmente la sbarretta sia perpendicolare all'asse z (dovrebbe essere il valor massimo di  ); successivamente una massa sale e l'altra scende ed
); successivamente una massa sale e l'altra scende ed  diminuisce. Prima di arrivare a 0, cioè a sovrapporsi all'asse z, dovrebbe arrivare al minimo di
diminuisce. Prima di arrivare a 0, cioè a sovrapporsi all'asse z, dovrebbe arrivare al minimo di  . ma, anche perchè
. ma, anche perchè  sarebbe ad un estremo,
sarebbe ad un estremo, 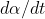 dovrebbe annullarsi insieme a
dovrebbe annullarsi insieme a 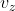 e
e 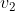 (la velocità diventerebbe
(la velocità diventerebbe 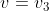 ) e però farebbero crash le equazioni da cui secondo il tuo penultimo post dovrei dedurre il valor minimo di
) e però farebbero crash le equazioni da cui secondo il tuo penultimo post dovrei dedurre il valor minimo di . E' un giochino intrigante....
. E' un giochino intrigante.... 


-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 250. Cariche, sbarretta e campo magnetico.
In realtà è più semplice di così: senza usare la ) che si ottiene integrando la formula dei post precedenti, come puoi esprimere
che si ottiene integrando la formula dei post precedenti, come puoi esprimere ) ? Bastano osservazioni geometriche.
? Bastano osservazioni geometriche.
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 250. Cariche, sbarretta e campo magnetico.
Dette x e Z le coordinate di m risulta alfa = arctg x/Z derivando rispetto a t verrebbe il minimo a 45 gradi
