La numerazione è riservata ai problemi della staffetta (chi risolve l'

-esimo, posta l'
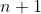
esimo), perciò ti chiedo di modificare il titolo.
Quanto alla soluzione del tuo problema, ricorda che
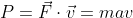
in una dimensione. Separando le variabili e integrando una volta (oppure direttamente ricordando chd
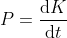
) ottieni
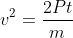
. Con un ulteriore passaggio puoi trovare anche
)
e quindi

in funzione di
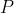
,
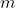
e della lunghezza

da percorrere. Queste due ultime quantità non variano, per cui differenziando l'espresisone trovi la relazione fra

,
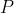
,
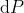
e
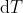
.
Se non sono stato abbastanza chiaro, dimmelo.
