Io ho trovato due modi per il calcolo della differenza di pressione tra interno ed esterno, non so se ce ne siano altri.
1) L'allungamento della circonferenza vale
)
, perciò la tensione nella gomma è
)
. Consideriamo una stretta striscia del tubo, parallela al tubo stesso e sottesa da un angolo
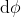
. Se consideriamo le tensioni alle due estremità "laterali" della striscia, ciascuna ha una componente
)
radiale, perciò abbiamo che la forza normale agente su questa striscia è
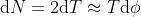
, agente verso l'interno. L'area della striscia è
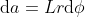
, perciò, essendo
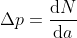
, otteniamo che la differenza di pressione fra interno ed esterno è
}{Lr})
2) Sfruttiamo un'altra definizione di
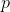
, come incremento di energia meccanica per unità di volume (pensiamo a
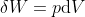
in termodinamica):
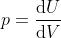
. L'incremento infinitesimo di volume è
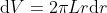
, mentre, essendo l'energia che consideriamo quella elastica nella gomma, si ha
^2)
, perciò
\text{d}r)
. Pertanto risulta semplicemente
\text{d}r}{2\pi L r \text{d}r}=\frac{2\pi k (r-R)}{Lr})
. Ho sottinteso il delta ma credo sia comunque chiaro che questa è la differenza fra le pressioni interna ed esterna.
Purtroppo il primo metodo richiederebbe un'immagine per essere visualizzato bene, spero comunque di essermi spiegato.
