Oltre alla radiazione cosmica di fondo di fotoni ne è presente una di neutrini, ad una temperatura effettiva
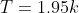
.
Stimare la densità di neutrini ed antineutrini per metro cubo.
I neutrini sono Fermioni: obbediscono al principio di indeterminazione di Pauli. Non è possibile che due occupino lo stesso stato quantico: si può dimostrare che la distribuzione del numero medio di stati occupati da neutrini di energia
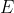
è

. Si tratta della statistica di Fermi-Dirac, dove il potenziale chimico è nullo (per curiosità, è dovuto al fatto che coppie neutrino-antineutrino venivano create liberamente e quindi il numero totale considerato non è fisso). Un esempio di distribuzione più familiare è quella di Maxwell-Boltzmann.
Qui una distribuzione nello spazio delle fasi
 )
formato da posizioni e quantità di moto è una funzione
})
tale che
} \, dx \, dy\, dz\, dp_x \, dp_y \, dp_z )
è il numero di punti all'interno dell'elemento di volume
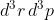
centrato in
)
(con naturale cambio di notazione). Non si tratta di infinitesimi, ma elementi di volume
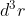
e
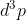
(questo nello spazio delle quantità di moto) finiti che contengono un grande numero di molecole pur essendo "puntiformi" rispetto a dimensioni macroscopiche.
Approssimiamo quindi la sommatoria sui vari elementi di volume in cui è diviso lo spazio delle fasi con
} \, d^3r \,d^3p )
.
Si può dimostrare (l'ho presente nel caso della radiazione di corpo nero) che l'elemento unidimensionale

contiene

stati, con
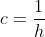
. Purtroppo di solito non viene data alcuna giustificazione del fattore
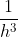
se non dimensionale (anche perché la suddivisione dello spazio delle fasi in elementi di volumi ha una certa arbitrarietà, vedi paragrafo precedente).
Assumere che i neutrini abbiamo massa trascurabile (quindi dalla relatività
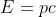
) e che ne esistano tre specie.
P.S: dopo vari mesi era il momento di riportare in vita la staffetta con un'azione decisa, spero non dispiaccia

.
Può essere utile sapere che
^{n+1}} )
. I primi termini sono sufficienti per avvicinarsi molto al valore a cui converge nel caso del problema.
Bonus: dimostrare quest'identità (nonostante le apparenze non è difficile!).

