punto b)
Per dimostrare che la densità di carica rimane costante considero il volume compreso tra due superfici sferiche di raggio
>r_{2}(t))
e dimostro che ad ogni istante la densità di carica non dipende da
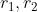
ma soltanto dal tempo. (e da altri costanti)

ovviamente
^3-r_{2}(t)^3)}{3})
Inoltre per il punto a) la carica compresa tra i due strati non varia ed e' proprio pari alla carica al tempo
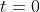
^3-r_{2}(0)^3)}{\frac{4 \pi}{3} R^3} = \frac{Q (r_{1}(0)^3-r_{2}(0)^3)}{ R^3})
Segue che
^3-r_{2}(0)^3)}{4 \pi( r_{1}(t)^3-r_{2}(t)^3)R^3})
Non mi resta che trovare l'equazione del moto di una superficie sferica.
Per il punto a) dato che la carica dentro la superficie rimane la stessa (e considerando una particella di carica q e massa m sulla superficie della sfera considerata) posso dire che:
=\frac{qQ_{r'<r}}{r(t)^2}=\frac{qQr(0)^3}{r(t)^2 R^3})
Non riesco a risolvere l'equazione differenziale però sicuramente sostituendo osservo che dipende da
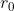
che è proprio quello che ci interessa infatti nella funzione della densità si semplifica tutto e rimane solo una funzione che dipende da costanti e da una funzione
)
in cui compare il tempo
^3-f_{2}(t)^3)R^3})
e ovviamente sono sicuro che in
)
o in
)
non compare in nessun modo il raggio iniziale
edit credo che l'ultimo pezzo sia sbagliato perchè dovrei dimostrare anche che
 = f_{2}(t))
(altrimenti non posso raccogliere e semplificare) credo si possa fare perchè alla fine tutte le altre quantità in gioco non dipendono dalla distanza dal centro
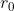
, allora
per
.