Buongiorno a tutti, è il mio primo messaggio su questo forum, spero di aver fatto tutto correttamente. Dato che volevo tentare il test di ammissione alla Normale mi sto esercitando con gli esercizi degli anni scorsi e volevo chiedere se mi potete aiutare con il problema 2 della prova di matematica dell'anno scorso. Cito qui il testo:
Inizialmente ho provato a uguagliare rx+sx = min(alfa*x+beta*y,gamma*x+delta*y) e facendo l'ipotesi che alfa*x+beta*y < gamma*x+delta*y ho messo in sistema rx+sx = alfa*x+beta*y e alfa*x+beta*y < gamma*x+delta*y, arrivando a r < alfa*(2s-beta-delta)/(s+delta) + gamma*(beta-s)/(s+delta). A questo punto ho provato a mettere t = (2s-beta-delta)/(s+delta) e vedere se 1-t = (beta-s)/(s+delta) usciva un'identità, ma mi esce come risultato che -beta = beta. Poteva essere un'idea questo procedimento?
Grazie in anticipo per l'aiuto.
SNS 2017 n. 2 (matematica)
Re: SNS 2017 n. 2 (matematica)
Premetto che non ho trovato io la soluzione del problema, ma sono stato aiutato. Comunque se vuoi ti do dei consigli.
Innanzitutto si tratta di un problema di geometria analitica nello spazio, non di algebra,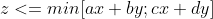 è l'insieme di punti che sta al di sotto del minimo tra i due piani ovvero è un angolo diedro.
è l'insieme di punti che sta al di sotto del minimo tra i due piani ovvero è un angolo diedro.
Devi dimostrare 1) che i due piani iniziali si intersecano 2) che il terzo piano passa per la retta di intersezione dei primi due.
Da queste due proprietà arrivi alla soluzione (tre piani che si intersecano in una retta sono in combinazione lineare).
Innanzitutto si tratta di un problema di geometria analitica nello spazio, non di algebra,
Devi dimostrare 1) che i due piani iniziali si intersecano 2) che il terzo piano passa per la retta di intersezione dei primi due.
Da queste due proprietà arrivi alla soluzione (tre piani che si intersecano in una retta sono in combinazione lineare).
