Pagina 1 di 1
Sns 1994-5
Inviato: 3 lug 2018, 13:39
da .Ruben.
Due cilindri uniformi ruotano indipendentemente intorno ai loro assi. Indichiamo con R_1,M_1 ed R_2,M_2 raggio e massa dei due cilindri. Supponiamo poi che i due assi di rotazione siano paralleli e che la rotazione avvenga nello stesso senso con velocità angolari ω_1 e ω_2 rispettivamente.
I due cilindri vengono quindi spostati fino a farli accostare e i loro assi sono mantenuti nella posizione schematizzata in figura. In questa posizione, essi sono liberi di ruotare intorno al proprio asse e rotolano senza strisciare lungo una tangente. Si calcoli la velocità angolare finale di ogni cilindro.
Re: Sns 1994-5
Inviato: 5 lug 2018, 10:15
da Aleksej99
Non agendo forze esterne sul sistema il momento angolare totale si conserva e dunque dette
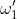
e
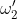
le velocità angolari finali dei due corpi si avrà
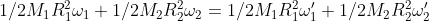
dalla condizione di non slittamento si ha che
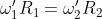
Svolgendo diligentemente i calcoli e detti
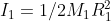
,

si ottiene
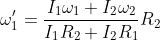
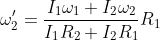
Re: Sns 1994-5
Inviato: 5 lug 2018, 13:30
da Dudin
Correggetemi se sbaglio ma secondo me il momento angolare non si conserva e bisogna sfruttare che:
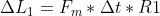
e che
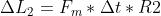
da cui
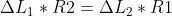
Re: Sns 1994-5
Inviato: 5 lug 2018, 13:31
da Dudin
per il resto direi che la mia soluzione e' identica ma il risultato esce leggermente diverso
Re: Sns 1994-5
Inviato: 6 lug 2018, 8:29
da .Ruben.
Ecco é come la mia.
Ora c'è un problema, i cilindri per non slittare alla fine devono muoversi in versi opposti, quindi le velocitá angolari finali devono avere segni diversi. Ma, se provi a farlo, ottieni un meno orrendo a denominatore
Re: Sns 1994-5
Inviato: 13 lug 2018, 16:30
da nicarepo
Il dubbio è ingiustificato in quanto la risposta proposta sopra è evidentemente corretta. Nonostante ciò ad essere rigorosi si dovrebbe fare la seguente considerazione.
Supponiamo che i momenti di inerzia dei due cilindri siano diversi e che inizialmente ruotino nello stesso senso. Dopo il contatto (senza strisciamento) uno dei due cilindri inverte la rotazione, affinché la velocità tangenziale nel punto di contatto sia uguale in modulo e verso per entrambi i corpi.
A questo punto la conservazione si può scrivere così:
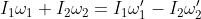
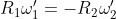
Da cui le formule trovate in precedenza (con
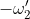
)
Re: Sns 1994-5
Inviato: 14 lug 2018, 12:25
da .Ruben.
Continuo a non essere d'accordo.
Scriviamolo coi vettori e poi con i moduli:
Il momento angolare (diretto lungo l'asse verticale) all'inizio vale:
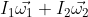
.
Alla fine (supponendo che il disco col secondo indice inverta la rotazione) il momento angolare vale:
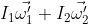
.
Prendendo i moduli (ossia moltiplicando scalarmente per il versore verticale nella direzione positiva):
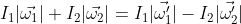
.
A questo punto il modulo della velocità nel punto di contatto vale:
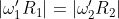
da cui:
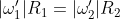
. Il problema di segno rimane (se i dischi sono identici si ha una singolarità).
Altro ragionamento (SUPPONENDO I DISCHI IDENTICI):
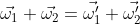
Siano
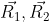
i vettori che collegano i centri di massa dei dischi al punto di contatto: ovviamente
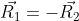
.
La velocità nel punto di contatto vale:

, da cui:
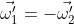
(e si ha ancora qualcosa di assurdo).
Re: Sns 1994-5
Inviato: 16 lug 2018, 1:44
da Avancini
xyz
Re: Sns 1994-5
Inviato: 16 lug 2018, 6:05
da .Ruben.
Se mi dici che N invece di una forza é un impulso, allora finalmente mi trovo.