154. Camini cadenti
154. Camini cadenti
Un camino, di lunghezza  e larghezza
e larghezza 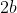 tali che
tali che 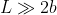 , inizialmente dritto, viene spinto leggermente e inizia a cadere, mantenendo il contatto col terreno. Trova la distanza dalla base del punto in cui si romperà con più facilità.
, inizialmente dritto, viene spinto leggermente e inizia a cadere, mantenendo il contatto col terreno. Trova la distanza dalla base del punto in cui si romperà con più facilità.
Re: 154. Camini cadenti
Suppongo che con 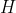 tu abbia equivalentemente indicato
tu abbia equivalentemente indicato  e con
e con  l'altezza del punto di rottura dalla base. In verità dovrebbe venire
l'altezza del punto di rottura dalla base. In verità dovrebbe venire 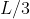 ...
...
Controlla se tipo hai considerato l'altezza dalla punta o cose del genere. Altrimenti potrei immaginare che tu abbia fatto il problema imputando la rottura ad una forza tangenziale (cosa che fornisce come risultato quel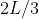 ). In realtà si può dimostrare che questa forza tangenziale è molto minore della tensione radiale lungo la sbarra, ed è dunque questa forza che causa la rottura.
). In realtà si può dimostrare che questa forza tangenziale è molto minore della tensione radiale lungo la sbarra, ed è dunque questa forza che causa la rottura.
Dato che ci sono metto anche un hint di modellizzazione: si provi a considerare il camino come due blocchi di altezza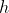 e
e 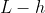 , dove
, dove 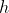 è l'altezza del punto di rottura dalla base, uniti da due aste ideali.
è l'altezza del punto di rottura dalla base, uniti da due aste ideali.
Controlla se tipo hai considerato l'altezza dalla punta o cose del genere. Altrimenti potrei immaginare che tu abbia fatto il problema imputando la rottura ad una forza tangenziale (cosa che fornisce come risultato quel
Dato che ci sono metto anche un hint di modellizzazione: si provi a considerare il camino come due blocchi di altezza
Re: 154. Camini cadenti
Io partendo dall'idea del tuo hint avevo trovato che le due forze rispettivamente tangenziale e radiale sono ;
)
 \bigl ( \bigl ( 5 + 3 \frac{r}{H} \bigr ) cos \theta - 3 \bigl ( 1+ \frac{r}{H} \bigr) \bigr ) \pm \frac{ mgH sin \theta} {8b} \frac{r}{H} \bigl ( 1 - \frac{r}{H} \bigr )^2)
La prima che era quella che avevo preso in considerazione io, la seconda è la trasversale che dici tu ma non mi sembra avere un massimo per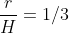 .
.
Sono abbastanza sicuro delle formule, se vuoi posto anche i conti, magari non ho usato qualche approssimazione ...
edit: ho corretto la forza radiale, che varia a seconda se la si consideri a sinistra o destra ... nelle approssimazioni del testo è significativo nella forza radiale solo il secondo addendo che ha in effetti un massimo per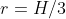
La prima che era quella che avevo preso in considerazione io, la seconda è la trasversale che dici tu ma non mi sembra avere un massimo per
Sono abbastanza sicuro delle formule, se vuoi posto anche i conti, magari non ho usato qualche approssimazione ...
edit: ho corretto la forza radiale, che varia a seconda se la si consideri a sinistra o destra ... nelle approssimazioni del testo è significativo nella forza radiale solo il secondo addendo che ha in effetti un massimo per
Ultima modifica di Aleksej99 il 2 lug 2018, 17:33, modificato 1 volta in totale.
Re: 154. Camini cadenti
Aleksej potresti postare i conti? A me viene 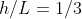 ma con equazioni diverse dalle tue. La prima differisce solo di coefficienti mi pare, ma la seconda proprio di forma. In particolare sfruttando l'ipotesi
ma con equazioni diverse dalle tue. La prima differisce solo di coefficienti mi pare, ma la seconda proprio di forma. In particolare sfruttando l'ipotesi 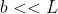 mi si semplifica molto.
mi si semplifica molto.
Re: 154. Camini cadenti
Ho corretto il post precedente ed ora ottengo il risultato giusto, quando posso posto il procedimento ma puoi farlo prima tu e mandare avanti la staffetta ...
Re: 154. Camini cadenti
Posto la mia soluzione anche se avviso che non ho ancora in mente un problema 155, quindi in caso tu lo avessi ti lascio senza problemi il testimone!
Come diceva Marcus, consideriamo il camino spezzato in due parti una di lunghezza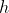 e un'altra
e un'altra 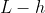 . Sulla parte
. Sulla parte 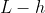 agiscono la forza peso relativa a quella parte e le due tensioni sulle aste ideali che possiamo scomporre in due componenti radiali (
agiscono la forza peso relativa a quella parte e le due tensioni sulle aste ideali che possiamo scomporre in due componenti radiali (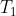 e
e 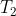 e due tangenziali (
e due tangenziali (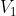 e
e 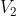 ).
).
Calcoliamo intanto velocità angolare e accelerazione angolare di tutto il camino in funzione di .
.
Dal momento della forza peso e conservazione dell'energia otteniamo:
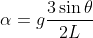 e
e }{L} )
Scriviamo quindi le forze e il momento sul pezzo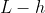 considerando che il suo cdm si muove lungo una circonferenza di raggio
considerando che il suo cdm si muove lungo una circonferenza di raggio 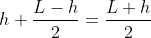 :
:
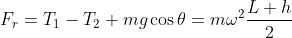
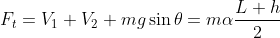
b-(V_{1}+V_{2})(\frac{L-h}{2})= \frac{1}{3}m \frac{(L-h)^2}{4} \alpha)
Dove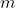 è la massa solo della parte lunga
è la massa solo della parte lunga 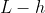 ed è pari a
ed è pari a M) .
.
Sostituendo le espressioni di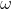 ,
,  e
e 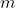 alle tre equazioni di sopra si ottiene:
alle tre equazioni di sopra si ottiene:
Mg \cos \theta=(1-\frac{h}{L})M \frac{3g(1-\cos \theta)}{L} \frac{L+h}{2} )
Mg \sin \theta= (1-\frac{h}{L})M g \frac{3\sin \theta}{2L} \frac{L+h}{2})
b-(V_{1}+V_{2})(\frac{L-h}{2})= \frac{1}{3} \frac{(1-\frac{h}{L})^3L^2}{4} Mg \frac{3\sin \theta}{2L})
Risolvendo si ha:
)
+T_{2})
Andando a sostituire nella terza si ottiene:
^3+\frac{MgL}{8} \sin \theta (1-\frac{h}{L})(4\frac{h}{L}-3\frac{h^2}{L^2}-1)-\frac{Mg}{2}(3L^2-5L^2 \cos \theta -3 h^2+3h^2 \cos \theta +2hL \cos \theta)\frac{b}{L^2})
Nelle ipotesi del problema l'ultimo termine della somma è trascurabile. Quindi si ha:
^2)
E quest'ultima ha proprio un massimo per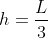 !
!
Sperando che non ci siano typo qua e la, dovrebbe essere tutto!
Come diceva Marcus, consideriamo il camino spezzato in due parti una di lunghezza
Calcoliamo intanto velocità angolare e accelerazione angolare di tutto il camino in funzione di
Dal momento della forza peso e conservazione dell'energia otteniamo:
Scriviamo quindi le forze e il momento sul pezzo
Dove
Sostituendo le espressioni di
Risolvendo si ha:
Andando a sostituire nella terza si ottiene:
Nelle ipotesi del problema l'ultimo termine della somma è trascurabile. Quindi si ha:
E quest'ultima ha proprio un massimo per
Sperando che non ci siano typo qua e la, dovrebbe essere tutto!
Re: 154. Camini cadenti
Va bene, che si vada col prossimo! 
