Penso che le nostre soluzioni differiscano per un motivo di fondo, più che per la risoluzione della ricorsione. Il risultato che avevo messo ieri era per un circuito di 20 semicerchi, ora l'ho fatto su Wofram con 46 semicerchi e il risultato è contenuto comunque nell'incertezza:
Non è così veloce fare il calcolo, dato che da solamente i primi 9 valori della ricorsione e per ottenere gli altri devo continuamente spostare lo zero; altrimenti avrei provato anche con 1000.
Ecco il mio procedimento.
Il valore della resistenza da 1m è:
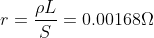
Quella dei semicerchi, in funzione di n, ponendo n=1 per il primo è:
 = 0.002639 (n+1) )
Immaginiamo ora di avere un circuito con
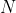
semicerchi, faremo poi tendere (quando mai)
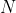
a infinito.
Sia
)
la resistenza equivalente dei primi
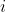
moduli (un semicherchio e un segmento), a partire dall'alto con
= r + R_N)
Il nostro obiettivo sarà quindi trovare
)
, che è la resistenza equivalence dell'intero circuito. Purtroppo Wolfram non ci da la formula per un N generico, quindi dovremo scegliere noi fin dall'inizio che numero prendere.
Per quanto detto prima, la ricorsione sarà allora:
 = r+ \frac{1}{\frac{2}{R_1 (N+2-i)} + \frac{1}{A(i)}} )
Con
= r + R_N= r+ \frac{\pi \rho L}{2S} (n+1) )
.
Scrivendo tutto con i valori numerici:
 =0.00168+ \frac{1}{\frac{1}{0.002639(N+2-i)} + \frac{1}{A(i)}} )
Con
= 0.00168 + 0.002639 (N+1) )
.
"No, no, you're not thinking; you're just being logical. "
