Dato che questo problema mi ha stuzzicato scrivo i miei ragionamenti. Non ho ottenuto il risultato giusto, puoi dirmi cosa ho sbagliato e in che direzione devo cercare? Non so se avro' tempo di riprovarci durante la settimana, invito altri a provarci perche' e' un problema interessante.
Fatto 1: l'energia si conserva. Abbastanza ovvio dato che la corda non striscia sul palo e non c'e' altro modo di perdere energia.
Fatto 2: il momento angolare
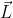 non
non si conserva. Se si conservasse, la velocita' finale della pallina sarebbe infinita se trascuriamo la dimensione del palo, o comunque molto grande se non la trascuriamo.
Il fatto 2 mi mette sull'allerta che questo problema e' piu' insidioso di quel che sembra. Probabilmente il problema richiede di usare le approssimazioni suggerite in qualche parte della soluzione ma poi non usarle in una qualche altra parte. Il semplice fatto che la pallina scende ovviamente vuol dire che il moto non e' circolare; ma potrebbe essere necessario considerare qualcosa di piu' complicato che solo quel fatto.
Proviamo ad assumere che
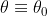
sia costante. A vedere video su Youtube dei tetherballs, sembra plausibile. Chiamiamo

,
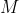
,
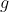
tensione, massa della pallina, gravita'. Chiamiamo

la lunghezza della corda all'istante iniziale (quando ancora niente si e' avvolto al filo). Il moto e' in un qualche senso circolare per cui non c'e' forza verticale, e la forza orizzontale serve solo a darmi l'accelerazione centrifuga. Quindi:
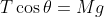
)
Facciamo due conti e troviamo
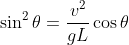
.
Alla fine del moto, una quantita'

di corda si e' avvolta al palo e da considerazioni geometriche l'altezza e' diminuita di
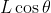
. La conservazione dell'energia da':
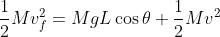
)
Mettendolo nella formula sopra troviamo:

Da cui
)
, da cui
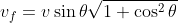
.
Che e' il risultato sbagliato. Possibili magagne:
1. Potrebbe essere falsa l'approssimazione che

e' costante, ma qualunque strategia per trovare
)
che posso immaginare richiede conti molto brutti e decisamente non olimpici. D'altra parte e' un problema da 4 stelle del Morin per cui puo' anche essere molto brutto.
2. Potrebbero essere sbagliate l'equazioni del moto qua sopra perche' l'approssimazione di moto circolare potrebbe non andar bene per quelle, ma allora uno dovrebbe introdurre un'altra variabile come lo spessore del palo, e le cose si complicano.
3. Questo dubbio mi è sorto leggendo qualcosa su internet mentre cercavo la soluzione a questo problema: le "considerazioni geometriche" di cui sopra potrebbero essere sbagliate e la relazione tra
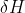
e
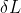
potrebbe essere piu' brutta, ma un po' mi stupirei. Se e' cosi' potresti spiegare per bene come si arriva alla relazione corretta?
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
