A) Una pallina da tennis con (piccola) massa
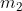
si trova sulla cima di una palla da basket con (grande) massa
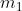
. Il punto più basso della palla da basket si trova ad altezza
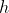
dal suolo e il punto più basso della pallina da tennis ad altezza
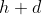
dal suolo (insomma,
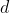
è il diametro della pallina grande).
Le due palline vengono lasciate cadere.
Nell'approssimazione che
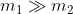
e che tutti gli urti siano elastici, a che altezza rimbalza la pallina da tennis?
B) Generalizziamo! Consideriamo

palline, chiamiamole
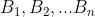
, aventi masse
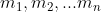
(con approssimazione
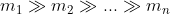
) poste in pila una sopra l'altra. Il punto più basso di
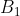
si trova ad altezza
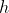
ed il punto più basso di
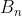
si trova ad altezza
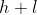
dal suolo.
Tutte insieme vengono lasciate cadere.
Considerando tutti gli urti elastici, a che altezza rimbalza la pallina più in alto?