Hint: Un suggerimento può essere quello di fare i calcoli un istante dopo l'inizio del moto, usando il teorema lavoro-energia.
113. Ancora aste!
113. Ancora aste!
Quattro aste omogenee identiche sono connesse da quattro giunti a snodo per formare un bellissimo quadrato, che viene poi posto, con delicatezza, su un tavolo liscio. Un vertice (P) è spinto nella direzione della diagonale del quadrato che passa per quel punto e, di conseguenza, aquista un'accelerazione iniziale 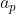 . In quale direzione e con quanta accelerazione inizia a muoversi il vertice Q opposto?
. In quale direzione e con quanta accelerazione inizia a muoversi il vertice Q opposto?
Hint: Un suggerimento può essere quello di fare i calcoli un istante dopo l'inizio del moto, usando il teorema lavoro-energia.
Hint: Un suggerimento può essere quello di fare i calcoli un istante dopo l'inizio del moto, usando il teorema lavoro-energia.
"No, no, you're not thinking; you're just being logical. "
Re: 113. Ancora aste!
Anche se non ho ancora trovato il modo di sfruttare il tuo suggerimento, potrebbe essere  (cioè Q accelera lungo la diagonale su cui agisce la forza ma in verso opposto a P)?
(cioè Q accelera lungo la diagonale su cui agisce la forza ma in verso opposto a P)?
Re: 113. Ancora aste!
Il segno meno è giusto, ma il modulo l'accelerazione no. Per usare il teorema lavoro energia, ti calcoli il lavoro fatto dalla forza in un tempo 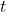 in funzione anche di
in funzione anche di 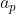 . Poi ti ricavi l'energia calcolando prima ad esempio la velocità del centro di massa delle quattro aste in funzione della velocità di p che puoi mettere in funzione di
. Poi ti ricavi l'energia calcolando prima ad esempio la velocità del centro di massa delle quattro aste in funzione della velocità di p che puoi mettere in funzione di 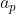 e della velocità angolare
e della velocità angolare 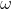 che è incognita.
che è incognita.
"No, no, you're not thinking; you're just being logical. "
Re: 113. Ancora aste!
Sì infatti ho trovato un errore di segno nei miei calcoli, ho rifatto tutto e ora mi viene 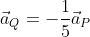 , utilizzando quindi la stessa strada di prima. Ora provo a rifare il tutto seguendo il tuo suggerimento.
, utilizzando quindi la stessa strada di prima. Ora provo a rifare il tutto seguendo il tuo suggerimento.
Re: 113. Ancora aste!
Giusto! Sono curioso di vedere quest'altro modo 
"No, no, you're not thinking; you're just being logical. "
Re: 113. Ancora aste!
È il modo più prolisso che si possa immaginare. In pratica ho considerato come asse x la diagonale PQ, come asse y l'altra, e come angolo  quello tra le sbarrette e l'asse y, e poi ho scritto
quello tra le sbarrette e l'asse y, e poi ho scritto 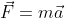 scomposta sui due assi e
scomposta sui due assi e 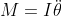 per due delle quattro sbarrette (in particolare due che giacciono dallo stesso lato rispetto a PQ), ottenendo sei equazioni in sei incognite, che sono sufficienti per risolvere il problema se se ne considerano le simmetrie: il sistema è simmetrico rispetto all'asse PQ, e di conseguenza le forze con cui interagiscono le aste nei punti P e Q non possono avere componenti lungo x, ma solo lungo y, perché altrimenti il terzo principio della dinamica non rispetterebbe la simmetria del sistema. Non si può dire lo stesso per la forza di interazione negli altri due vertici perché, a causa della forza esterna, il sistema non è simmetrico rispetto alla diagonale passante per questi due vertici, e quindi questa forza (che per simmetria deve essere la stessa in modulo in entrambi i vertici) avrà in generale una componente lungo x e una lungo y. Le sei incognite sono quindi la forza in P (
per due delle quattro sbarrette (in particolare due che giacciono dallo stesso lato rispetto a PQ), ottenendo sei equazioni in sei incognite, che sono sufficienti per risolvere il problema se se ne considerano le simmetrie: il sistema è simmetrico rispetto all'asse PQ, e di conseguenza le forze con cui interagiscono le aste nei punti P e Q non possono avere componenti lungo x, ma solo lungo y, perché altrimenti il terzo principio della dinamica non rispetterebbe la simmetria del sistema. Non si può dire lo stesso per la forza di interazione negli altri due vertici perché, a causa della forza esterna, il sistema non è simmetrico rispetto alla diagonale passante per questi due vertici, e quindi questa forza (che per simmetria deve essere la stessa in modulo in entrambi i vertici) avrà in generale una componente lungo x e una lungo y. Le sei incognite sono quindi la forza in P (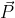 ), la forza in Q (
), la forza in Q (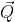 ), le due componenti della forza nel vertice in cui le due aste sono a contatto (
), le due componenti della forza nel vertice in cui le due aste sono a contatto (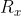 e
e 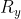 ), l'accelerazione angolare
), l'accelerazione angolare 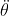 e la forza esterna
e la forza esterna 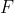 , che, per simmetria, è distribuita in parti uguali sulle due aste che si toccano in P. Per scrivere il sistema conviene esprimere le componenti delle accelerazioni dei centri di massa delle due aste in funzione dell'accelerazione di P (
, che, per simmetria, è distribuita in parti uguali sulle due aste che si toccano in P. Per scrivere il sistema conviene esprimere le componenti delle accelerazioni dei centri di massa delle due aste in funzione dell'accelerazione di P (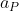 ):
):
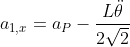
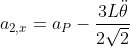
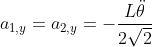
Il sistema quindi è:
 \\
\frac{L}{2 \sqrt{2}} (\frac{F}{2} + R_x + R_y - P) = \frac{ML^2}{12} \ddot{\theta} \\
R_y - Q = -M \frac{L \ddot{\theta}}{2 \sqrt{2}} \\
R_x = M (a_P - \frac{3L \ddot{\theta}}{2 \sqrt{2}}) \\
\frac{L}{2 \sqrt{2}} (R_x - R_y - Q) = \frac{ML^2}{12} \ddot{\theta}
\end{cases})
da cui si ottiene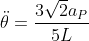 .
.
Quindi si ha:
 , dove ho sostituito, per l'ultima uguaglianza, l'espressione di
, dove ho sostituito, per l'ultima uguaglianza, l'espressione di 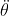 ricavata dal sistema.
ricavata dal sistema.
Il sistema quindi è:
da cui si ottiene
Quindi si ha:
Re: 113. Ancora aste!
Perfetto! A te la staffetta! 
"No, no, you're not thinking; you're just being logical. "
Re: 113. Ancora aste!
Siano le aste in senso antiorario PA,AQ,QB,BP e consideriamo l'angolo  formato dalla diagonale PQ con QB. La forza F applicata in P ha momento nullo rispetto a Q, così come le sue componenti
formato dalla diagonale PQ con QB. La forza F applicata in P ha momento nullo rispetto a Q, così come le sue componenti 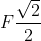 sulle aste PB e PA hanno momenti opposti: se il sistema fosse rigido non sarebbero possibili rotazioni attorno a Q. Ma essendoci gli snodi sono possibili come si vede rotazioni opposte che salvano la nullità del momento. Considerando per es. il braccio PBQ abbiamo
sulle aste PB e PA hanno momenti opposti: se il sistema fosse rigido non sarebbero possibili rotazioni attorno a Q. Ma essendoci gli snodi sono possibili come si vede rotazioni opposte che salvano la nullità del momento. Considerando per es. il braccio PBQ abbiamo
]+Ml^2/4].\frac {d^2\theta}{dt^2}= F l (\sqrt{2}/2)) ovvero
ovvero ) cioè
cioè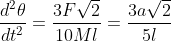
Allora l'accelerazione di B verso l'alto con retta d'azione PB risulta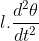 analogamente a quella di A verso destra con retta d'azione PA. Esse si compongono in P e danno come risultante, moltiplicando per
analogamente a quella di A verso destra con retta d'azione PA. Esse si compongono in P e danno come risultante, moltiplicando per 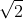 , proprio la acc. di P rispetto a Q cioè, invertendo il segno, quella di Q rispetto a P che risulta
, proprio la acc. di P rispetto a Q cioè, invertendo il segno, quella di Q rispetto a P che risulta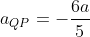 . Ma l'acc. assoluta di Q richiesta è l'acc. assoluta a di P + l'acc. relativa di Q rispetto a P e pertanto abbiamo
. Ma l'acc. assoluta di Q richiesta è l'acc. assoluta a di P + l'acc. relativa di Q rispetto a P e pertanto abbiamo
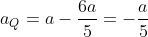



P.S. Ritengo questo procedimento molto semplice e razionale perchè non fa intervenire forze interne evitando le sei equazioni in sei incognite (!!) di Step98 o lo stesso procedimento energetico che gli aveva suggerito Flaffo sicuramente più complesso.
Allora l'accelerazione di B verso l'alto con retta d'azione PB risulta
P.S. Ritengo questo procedimento molto semplice e razionale perchè non fa intervenire forze interne evitando le sei equazioni in sei incognite (!!) di Step98 o lo stesso procedimento energetico che gli aveva suggerito Flaffo sicuramente più complesso.
Re: 113. Ancora aste!
Non sono sicuro che vada bene il tuo procedimento, per quanto presenti indubbi vantaggi.
Innanzitutto non riesco a capire questo: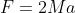 , ma non credo sia così, perché dalla risultante delle forze esterne puoi ottenere l'accelerazione del centro di massa, non quella del punto P, e infatti, anche se ottieni, per l'accelerazione angolare, la stessa espressione che ho ottenuto dal sistema del post precedente, puoi vedere che risolvendolo considerando l'accelerazione di P come incognita e la forza F come grandezza nota, si ottiene per l'accelerazione angolare in funzione di F
, ma non credo sia così, perché dalla risultante delle forze esterne puoi ottenere l'accelerazione del centro di massa, non quella del punto P, e infatti, anche se ottieni, per l'accelerazione angolare, la stessa espressione che ho ottenuto dal sistema del post precedente, puoi vedere che risolvendolo considerando l'accelerazione di P come incognita e la forza F come grandezza nota, si ottiene per l'accelerazione angolare in funzione di F 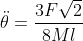 , che è diversa da quella che ottieni tu. Penso che il problema sia nel modo in cui hai applicato la seconda equazione della dinamica rotatoria: in pratica se scrivi
, che è diversa da quella che ottieni tu. Penso che il problema sia nel modo in cui hai applicato la seconda equazione della dinamica rotatoria: in pratica se scrivi 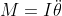 , sottintendi che i corpi stiano accelerando attorno al polo rispetto al quale stai calcolando i momenti, il che non è vero in questo caso perché, se così fosse, un istante di tempo infinitesimo
, sottintendi che i corpi stiano accelerando attorno al polo rispetto al quale stai calcolando i momenti, il che non è vero in questo caso perché, se così fosse, un istante di tempo infinitesimo 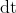 dopo la partenza il punto Q non dovrebbe avere acquisito alcuna velocità infinitesima, il che non è noto a priori ed è anche falso perché la sua accelerazione è proprio la grandezza che dobbiamo calcolare. In sostanza la seconda equazione andrebbe scritta nella forma più generale, cioè
dopo la partenza il punto Q non dovrebbe avere acquisito alcuna velocità infinitesima, il che non è noto a priori ed è anche falso perché la sua accelerazione è proprio la grandezza che dobbiamo calcolare. In sostanza la seconda equazione andrebbe scritta nella forma più generale, cioè 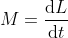 , che si riduce a
, che si riduce a 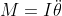 solo se si suppone che Q abbia accelerazione nulla.
solo se si suppone che Q abbia accelerazione nulla.
Innanzitutto non riesco a capire questo:
Come fai a passare al secondo membro? Sembra che sia implicitoguido ha scritto: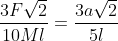
Re: 113. Ancora aste!
Rispondo da scuola e magari posso precisare anche meglio nel pomeriggio. Comunque non sono d'accordo. Per il teorema del centro di massa è la forza esterna che ne determina l'accelerazione e su questo credo che siamo tutti d'accordo. Ora il nostro sistema da questo punto di vista è in tutto e per tutto equivalente a quello in cui una massa 2M è concentrata in P e una massa 2M è concentrata in Q: infatti il cdm delle aste 1 e 4 è a metà fra P e cdm del sistema sulla diagonale e lo stesso avviene per 2 e 3 a metà fra Q e cdm sistema. Il cdm sistema non muta se queste masse 2M si spostano in P e Q. Ma in P si applica F che, dice il testo, produce inizialmente l'acc. a per P e quindi deve essere a= F/2M. Non capisco poi l'obiezione sulla rotazione attorno a Q. Le componenti di F come ho spiegato hanno momenti opposti rispetto a Q e determinano rotazioni opposte complessivamente nulle perchè il momento delle esterne è nullo. Se il sistema fosse rigido non ci sarebbe alcuna rotazione. Ma è proprio la natura del sistema con snodi che permette rotazioni opposte complessivamente nulle.
Questo è il mio punto di vista. Penso che un indizio della sua correttezza possa essere che il risultato è giusto senza considerare l'intervento della forza interne come deve poter essere....
Questo è il mio punto di vista. Penso che un indizio della sua correttezza possa essere che il risultato è giusto senza considerare l'intervento della forza interne come deve poter essere....
