curva e palloncino
curva e palloncino
Una macchina percorre una curva circolare di raggio  a velocità angolare costante
a velocità angolare costante 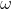 . All'nterno della macchina c'è un palloncino sferico di raggio
. All'nterno della macchina c'è un palloncino sferico di raggio  pieno d'elio (di densità
pieno d'elio (di densità 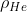 e collegato tramite un filo inestensibile e di massa trascurabile al pavimento della macchina. Calcolare l'angolo che il filo forma con la verticale durante la curva e la sua tensione. Si faccia l'approssimazione che le dimensioni della macchina siano trascurabili rispetto al raggio della curva.
e collegato tramite un filo inestensibile e di massa trascurabile al pavimento della macchina. Calcolare l'angolo che il filo forma con la verticale durante la curva e la sua tensione. Si faccia l'approssimazione che le dimensioni della macchina siano trascurabili rispetto al raggio della curva.
Re: curva e palloncino
mmmm attenzione........
da che parte deflette il palloncino secondo te?
da che parte deflette il palloncino secondo te?
-
FedericoC.
- Messaggi: 172
- Iscritto il: 8 feb 2016, 14:34
Re: curva e palloncino
Io ho supposto che il palloncino defletta verso l'esterno in modo tale che la tensione radiale possa fungere da forza centripeta
Re: curva e palloncino
stai dimenicando una forza...
ti consiglio comunque di metterti nel sistema non inerziale centrato nel centro della curva che ruoto insieme alla macchina.
E attento a considerare tutti gli effetti che la rotazione ha sul sistema.
P. S. ti do un aiutino dicendondoti che facendo tutto bene dovrebbe risultarti che il palloncino deflette verso l interno della curva
ti consiglio comunque di metterti nel sistema non inerziale centrato nel centro della curva che ruoto insieme alla macchina.
E attento a considerare tutti gli effetti che la rotazione ha sul sistema.
P. S. ti do un aiutino dicendondoti che facendo tutto bene dovrebbe risultarti che il palloncino deflette verso l interno della curva
Re: curva e palloncino
Ho ripensato a quel video di Smartereveryday..un palloncino d'elio in una macchina che accelera in avanti si inclina di un angolo  ,rispetto alla verticale, nella stessa direzione dell'accelerazione.... è chiaro, allora, che debba esistere,oltre a quella verticale, una forza di Archimede diretta in senso radiale in cui la
,rispetto alla verticale, nella stessa direzione dell'accelerazione.... è chiaro, allora, che debba esistere,oltre a quella verticale, una forza di Archimede diretta in senso radiale in cui la 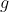 che comprare in nell'equazione della forza è sostituita dall'accelerazione della macchina in quell'istante. Pensando quindi al moto circolare della macchina, abbiamo un'accelerazione centrifuga radiale (verso destra, curva a sinistra) pari a
che comprare in nell'equazione della forza è sostituita dall'accelerazione della macchina in quell'istante. Pensando quindi al moto circolare della macchina, abbiamo un'accelerazione centrifuga radiale (verso destra, curva a sinistra) pari a 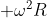 . Segue che la forza di Archimede in senso radiale, diretta verso sinistra, è:
. Segue che la forza di Archimede in senso radiale, diretta verso sinistra, è:
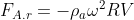
Dove è il raggio della curva. Questo è valido solo se la lunghezza
è il raggio della curva. Questo è valido solo se la lunghezza 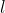 della corda è molto minore di
della corda è molto minore di  , altrimenti al posto di
, altrimenti al posto di  avremmo dovuto scrivere
avremmo dovuto scrivere 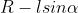 .
.
La forza totale in senso radiale si ottiene aggiungendo a quella di Archimede(negativa) il "peso" del palloncino in questa direzione, dato dalla forza centrifuga (positiva) e sommando la tensione della corda in questo verso(positiva):
 {\omega}^2 RV +Tsin\alpha)
La forza in verticale è, semplicemente:
gV-Tcos\alpha)
L'equilibrio del palloncino si ha per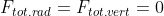
Sostituendo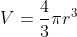 dove
dove  indica il raggio del palloncino, le due equazioni da cui si ottengono
indica il raggio del palloncino, le due equazioni da cui si ottengono  e
e  sono:
sono:
 {\omega}^2 R)
g)
Questo ragionamento, in generale è valido solo se la densità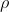 del gas nel palloncino soddisfa la condizione:
del gas nel palloncino soddisfa la condizione:
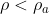
In caso contrario, per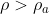 , la forza centrifuga supera, in modulo, la forza di Archimede in senso radiale e la forza risultante sarà positiva, cioè diretta all'esterno della curva e il palloncino si inclinerà di un angolo
, la forza centrifuga supera, in modulo, la forza di Archimede in senso radiale e la forza risultante sarà positiva, cioè diretta all'esterno della curva e il palloncino si inclinerà di un angolo  verso destra.
verso destra.
Dove
La forza totale in senso radiale si ottiene aggiungendo a quella di Archimede(negativa) il "peso" del palloncino in questa direzione, dato dalla forza centrifuga (positiva) e sommando la tensione della corda in questo verso(positiva):
La forza in verticale è, semplicemente:
L'equilibrio del palloncino si ha per
Sostituendo
Questo ragionamento, in generale è valido solo se la densità
In caso contrario, per
"No, no, you're not thinking; you're just being logical. "
Re: curva e palloncino
ok giusto bravo! sarebbe istruttivo peró far vedere formalmente perchè viene fuori questa forza verso l'interno anche perchè l'analogia con la forza di archimede, anche perchè se le dimensioni della macchina non sono trascurabili rispetto alla curva l'analogia porta a conclusioni sbagliate....
Re: curva e palloncino
Spero di aver capito cosa intendi.. fammi sapere se è giusto 
La forza su ciascun volume infinitesimale di elio nel palloncino è:
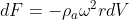
Dove indica la distanza del volume di elio dall'asse di rotazione (centro della curva). La forza totale esercitata dall'aria sul palloncino è, allora:
indica la distanza del volume di elio dall'asse di rotazione (centro della curva). La forza totale esercitata dall'aria sul palloncino è, allora:
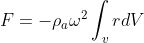
Se le dimensioni del palloncino sono trascurabili rispetto al raggio della curva, possiamo scrivere:
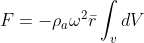
Dove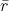 è la distanza del centro del palloncino dall'asse di rotazione, cioè:
è la distanza del centro del palloncino dall'asse di rotazione, cioè:
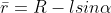
In generale, quindi, la legge di Archimede si può applicare solo se le dimensioni del palloncino sono trascurabili rispetto alla sua distanza dall'asse di rotazione.
P.s Se macchina fosse totalmente riempita di elio o di un gas più leggero dell'elio, il palloncino si inclinerebbe all'esterno della curva!
La forza su ciascun volume infinitesimale di elio nel palloncino è:
Dove
Se le dimensioni del palloncino sono trascurabili rispetto al raggio della curva, possiamo scrivere:
Dove
In generale, quindi, la legge di Archimede si può applicare solo se le dimensioni del palloncino sono trascurabili rispetto alla sua distanza dall'asse di rotazione.
P.s Se macchina fosse totalmente riempita di elio o di un gas più leggero dell'elio, il palloncino si inclinerebbe all'esterno della curva!
"No, no, you're not thinking; you're just being logical. "
Re: curva e palloncino
mmm si ok anche se quello che intendevo era proprio di spiegare perchè la forza sul volumetto di elio dV fosse quella. La legge di archimede vale per un campo di forze uniforme, cosa che qui non è vera quindi a priori nessuno ci assicura che l analogia funzioni ancora. Volevo più omeno che estendessi la dimostrazione che si fa per dimostrare la legge di archimede a un caso come questo dove il campo non è uniforme. 
Re: curva e palloncino
Scorrendo vari post in giro per il forum in questo periodo di ozio, ho ritrovato questo problema che avevo lasciato "irrisolto". Spero di aver compreso quello che intendevi.. 
Alla fine dimostrerò che la forza di Archimede è ancora valida solo se le dimensioni del palloncino sono piccole rispetto alla distanza palloncino-centro curva.
Modelliamo il palloncino come un rettangolo. Nel suo lato più vicino al centro della curva il valore della pressione e della densità dell'aria sono rispettivamente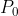 e
e 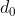 e
e 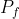 e
e 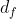 pressione e densita nel lato più lontano della curva. Inoltre la distanza tra i due lati è
pressione e densita nel lato più lontano della curva. Inoltre la distanza tra i due lati è  . L'accelerazione centrifuga è data da:
. L'accelerazione centrifuga è data da:
= \omega^2 (R+r))
Dove indica la distanza dal lato più vicino al centro della curva. Semplifichiamo leggermente il problema dicendo che la temperatura all'interno del palloncino è costante. Allora, dalla legge dei gas perfetti e dall'equilibrio delle forze su ogni rettangolo infinitesimo di aria otteniamo la seguendo equazione:
indica la distanza dal lato più vicino al centro della curva. Semplifichiamo leggermente il problema dicendo che la temperatura all'interno del palloncino è costante. Allora, dalla legge dei gas perfetti e dall'equilibrio delle forze su ogni rettangolo infinitesimo di aria otteniamo la seguendo equazione:
 dr)
Integriamo. Estremi di integrazione per P sono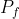 e
e 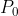 e per
e per  sono
sono  e
e  .
.
Otteniamo quindi:
}^2 - R^2\right)\right])
Ora entra in gioco l'approssimazione della forza nel caso in cui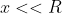 . In tal caso l'equazione precedente diventa:
. In tal caso l'equazione precedente diventa:
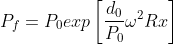
Ciò che sta dentro lesponenziale è molto piccolo. Taylor allora ci dice che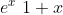 .
.
Abbiamo infine:
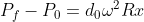
Che è esattamente la forza di Archimede. Tutto ciò ovviamente non vale per paragonabili a
paragonabili a  . In questo caso la forza sarebbe alquanto brutta (come abbiamo visto calcolandola), perché, oltre a variare l'acelerazione centrifuga in funzione dalla distanza dal centro, varia anche la densità dell'aria che deve essere considerata necessariamente compressibile.
. In questo caso la forza sarebbe alquanto brutta (come abbiamo visto calcolandola), perché, oltre a variare l'acelerazione centrifuga in funzione dalla distanza dal centro, varia anche la densità dell'aria che deve essere considerata necessariamente compressibile.
Alla fine dimostrerò che la forza di Archimede è ancora valida solo se le dimensioni del palloncino sono piccole rispetto alla distanza palloncino-centro curva.
Modelliamo il palloncino come un rettangolo. Nel suo lato più vicino al centro della curva il valore della pressione e della densità dell'aria sono rispettivamente
Dove
Integriamo. Estremi di integrazione per P sono
Otteniamo quindi:
Ora entra in gioco l'approssimazione della forza nel caso in cui
Ciò che sta dentro lesponenziale è molto piccolo. Taylor allora ci dice che
Abbiamo infine:
Che è esattamente la forza di Archimede. Tutto ciò ovviamente non vale per
"No, no, you're not thinking; you're just being logical. "
