Sono date due lenti sottili di lunghezze focali
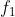
e
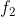
. Vengono messe su un banco ottico in modo da essere molto vicine tra loro, una dopo l'altra. Dimostrare che il sistema si comporta come se in quel punto ci fosse una sola lente con distanza focale
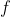
legata alle altre due da:
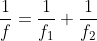
(non ditemi che questa relazione non vi ricorda niente)
Se volete ragionare un po' e soprattutto fare un po' di conti, potete provare anche ad affrontare il caso generale (parecchio più complicato), in cui tra le due lenti c'è una distanza
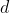
.
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)