Esprimo alcune considerazioni su questo problema.
L’inserimento di una successione di macchine di Carnot tra le due sorgenti A e B alle temperature
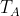
e
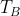
con
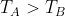
, impone che le stesse temperature siano inversamente proporzionali, cioè
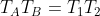
. Infatti differenziando la precedente relazione si desume l’equazione della generica macchina di Carnot. Quando A cede calore, la
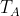
diminuisce e la
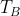
aumenta perché B acquista calore. Allorché
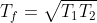
, i due corpi raggiungono la stessa temperatura e il motore termina il suo funzionamento. La
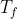
è la media geometrica delle temperature iniziali. Se i due corpi si ponevano a contatto senza motori termici, avrebbero conseguito la temperatura di equilibrio

, ossia la media aritmetica di
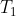
e
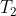
. Poiché la macchina ha trasferito dell’energia all’ambiente, ci aspettiamo che la temperatura finale
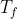
sia inferiore a Te. Ciò si verifica subito perché
^2-T_1T_2 = [(T_1-T_2)/2]^2>0)
. Dobbiamo osservare che Tf è la minima temperatura di equilibrio del sistema realizzabile con un motore termico, giacchè il lavoro estratto assume il valore più alto possibile. Se i corpi A e B si portano in equilibrio spontaneamente alla temperatura Te, essi non forniscono all’esterno alcun lavoro dato che
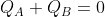
. Deriva che il lavoro prodotto dalle macchine
+mc(T_2-T_f) =2mc(T_e-T_f))
corrisponde proprio all’energia scaricata dalle due masse all’esterno se, partendo dalla temperatura di equilibrio, si portassero alla temperatura Tf.
Il rendimento dell’insieme di macchine vale:
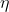
= 1- Qceduto/Qassorbito =
/(T_1-T_f) =1-\sqrt {T_2/T_1})
.
Da
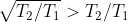
si ha che
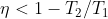
. Risulta che il rendimento della successione di macchine di Carnot è inferiore a quello del motore singolo di Carnot che agisce nell’istante iniziale. Ciò avviene perché il rendimento della macchina generica
)
diminuisce da
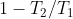
a zero al crescere di
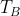
. Ecco perché il rendimento complessivo è intermedio tra i valori estremi degli
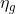
di tutte le macchine di Carnot che hanno operato tra A e B.
