data la funzione del potenziale
V(x,y,z)=Az^2+By+Ce^[(x+y)/L] con A,B,C e L costanti note
ricavare il lavoro fatto dalle forze del campo elettrostatico per spostare una carica q (nota) dal
punto P1(0,0,3) al punto P2(2,1,3)
la traccia è questa...io ho risolto il problema trovandomi prima la differenza di potenziale ΔV(p1p2)
e poi ho utilizzato la definizione della diff di potenziale ΔV=ΔU/q e quindi W=-qΔV
ora il mio prof per esercizio mi ha chiesto di calcolare lo stesso lavoro ricavando prima il campo e poi
risolvendo l'integrale tra p1 e p2 di di -E(scalare)ds
ho iniziato ricavandomi l'espressione del campo
E=-gradV
∂V(x,y,z)/∂x=C e^(x+y)/L x/L Ex=-C e^(x+y)/L x/L
∂V(x,y,z)/∂y=B+ C e^(x+y)/L y/L Ey=-[B+ C e^(x+y)/L y/L]
∂V(x,y,z)/∂z=2Az Ez=-2Az
quindi E(-C e^(x+y)/L x/L;-B- C e^(x+y)/L y/L;-2Az)
ora
ΔVp1p2=-∫(tra p1 e p2) di Escalaredl=-∫(tra p1 e p2) Exdx+Eydy+Ezdz
bisogna parametrizzare il percorso tra p2 e p1
x=0+2t x=2t
y=0+1t y=t
z=3 z=3
da queste relazioni bisogna calcolare i differenziali e poi integrare
mi potreste aiutare perchè nn so + andare avanti...grazie
esercizio elettrostatica
Re: esercizio elettrostatica
La derivata del potenziale rispetto a 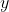 mi sembra sbagliata. Se non scrivi in latex, purtroppo il tuo messaggio diventa quasi illeggibile.
mi sembra sbagliata. Se non scrivi in latex, purtroppo il tuo messaggio diventa quasi illeggibile.
L'integrale lungo una curva vale:
 \cdot \gamma'(\vec{x}) dx})
Dove è il prodotto scalare. A te i conti.
è il prodotto scalare. A te i conti.
L'integrale lungo una curva vale:
Dove
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
