1) le condizioni su a affinché il moto circolare sia stabile
2) la frequenza delle piccole oscillazioni radiali riguardo a questo moto circolare
La forza di Yukawa
La forza di Yukawa
Una particella di massa m si muove su una circonferenza di raggio R sotto l'azione di una forza centrale attrattiva (Yukawa)
. Determinare:
1) le condizioni su a affinché il moto circolare sia stabile
2) la frequenza delle piccole oscillazioni radiali riguardo a questo moto circolare
1) le condizioni su a affinché il moto circolare sia stabile
2) la frequenza delle piccole oscillazioni radiali riguardo a questo moto circolare
-
DeoGratias
- Messaggi: 146
- Iscritto il: 2 nov 2020, 23:58
Re: La forza di Yukawa
Sia =-k\frac{e^{-\frac{r}{a}}}{r^2}\hat{r}=F_r \hat{r})
e )
il potenziale che dà origine a tale campo di forze, tale che 
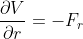
. Sfruttiamo il fatto che il moto di un corpo in un campo di forze centrale può essere ricondotto a un moto unidimensionale sotto l'azione di un potenziale efficace =V(r)+\frac{L^2}{2mr^2})
, dove 
è il modulo del momento angolare del corpo rispetto all'origine (si conserva, visto che sia la forza sia l'impulso sono radiali).
Se l'orbita è circolare e
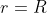
, si dovrà avere =0 \Rightarrow \frac{L^2}{mR^3}=-F_r(R)=k\frac{e^{-R/a}}{R^2})
.
L'orbita è stabile se >0)
. Calcoliamolo:
 = \frac{3L^2}{mR^4}-k\frac{e^{-R/a}}{R^2}\left ( \frac{2}{R}+\frac{1}{a} \right ))
Grazie alla condizione precedente, possiamo scriverlo come
=k\frac{e^{-R/a}}{R^3}\left( 1-\frac{R}{a} \right))
Quindi le orbite con
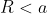
sono stabili.
Quando
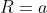
la derivata seconda si annulla, mentre la derivata terza è negativa, quindi tale orbita è instabile. Perciò le orbite stabili sono solo quelle trovate in precedenza. In tal caso, la frequenza delle piccole oscillazioni vale
}=\sqrt{\frac{k}{m}\frac{e^{-R/a}}{R^3}\left( 1-\frac{R}{a} \right)})
Per
la forza di Yukawa diventa quella newtoniana, e ritroviamo il fatto che tutte le orbite circolari sono stabili con frequenza di oscillazione pari a quella orbitale.
Se l'orbita è circolare e
L'orbita è stabile se
Grazie alla condizione precedente, possiamo scriverlo come
Quindi le orbite con
Quando
Per
Re: La forza di Yukawa
E' giusto e corretto il punto 1 sulla condizione di stabilità. Per quanto riguarda il punto 2 invece ti consiglierei di esporre il tuo procedimento per vedere se il tuo risultato, che attualmente è diverso da quello ufficiale (Cahn), è davvero conclusivo.