Il punto 1 ok, il punto 2 piu' o meno ok, ma sul 3 non sono d'accordo...
Fede:) ha scritto: ↑11 ago 2022, 22:10
si può supporre che tendenzialmente la velocità di ogni particella sia equipartita nelle 3 componenti, quindi anche gli scambi di energia sono equipartiti nelle 3 direzioni
Qua non sono d'accordo. Non c'e' necessariamente legame tra velocita' ed energia. Quando ho cominciato a pensare a questo problema mi interessava il risultato per un gas di fotoni in cui
)
dipende solo dalla temperatura
)
mentre la velocita' di tutte le particelle e' sempre

, e le "altre particelle" con cui interagiscono i fotoni sono, con ogni probabilita', non altri fotoni ma altre particelle che si trovano nello stesso spazio. Per certi aspetti e' anche piu' facile pensare a questo problema per un gas di fotoni che un gas normale, perche' tutte le particelle si muovono alla stessa velocita' cosi' neanche ci si deve preoccupare di che vuol dire "velocita' media", e non c'e' rischio di confondersi tra
)
e

. Comunque il risultato vale anche quando
)
e

sono legate.
Fede:) ha scritto: ↑11 ago 2022, 22:10
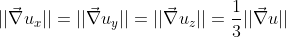
Non sono d'accordo neanche qua, innanzitutto
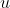
non e' un vettore quindi assumo che per
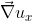
intendi
_x)
ma non e' che sia cosi' chiara come notazione.
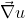
va da zone di alta energia a zone di bassa energia, se orienti l'asse
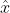
lungo
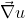
avrai che
_y = (\vec \nabla u)_z = 0)
.
E poi, in ogni caso, quel fattore

non capisco da dove verrebbe fuori. Se
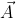
e' un vettore,
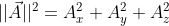
quindi se avessi
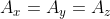
, avresti che
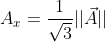
, non
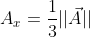
.
Fede:) ha scritto: ↑11 ago 2022, 22:10
si può supporre che tendenzialmente la velocità di ogni particella sia equipartita nelle 3 componenti
quindi anche gli scambi di energia sono equipartiti nelle 3 direzioni
Forse e' qui la confusione; la prima frase e' vera, almeno localmente, ovvero possiamo approssimare che le particelle che partono da uno stesso punto
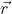
partano in tutte le direzioni, portando tutte in media la stessa energia e avendo la stessa velocita'. Ma lo scambio di energie dovuto a queste non e' equipartito; quelle che si muovono nella direzione di
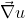
, e poi vengono assorbite nella posizione
)
, depositano li' meno energia di quella che e' stata persa dalle particelle partite da quel punto. Quelle che si muovono in direzione opposta e arrivano in
)
, depositano li' meno energia delle particelle che se ne sono appena andate da quel punto.
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
