278 - Carica sul cono
278 - Carica sul cono
Una carica 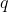 è posta sul vertice di un cono di apotema
è posta sul vertice di un cono di apotema 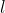 e di densità di carica superficiale
e di densità di carica superficiale 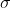 . Ora, supponiamo di sezionare il cono a
. Ora, supponiamo di sezionare il cono a  e di rimuovere la parte superiore: qual è la forza agente sulla carica
e di rimuovere la parte superiore: qual è la forza agente sulla carica 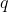 dovuta alla parte inferiore del cono? Determinare inoltre per quale angolo
dovuta alla parte inferiore del cono? Determinare inoltre per quale angolo  essa è massima, detto
essa è massima, detto  l'angolo di apertura del cono
l'angolo di apertura del cono
Ultima modifica di Rick il 25 nov 2021, 18:10, modificato 1 volta in totale.
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: Carica sul cono
La carica 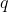 sia posta nell'origine di un sistema di coordinate sferiche e l'asse delle
sia posta nell'origine di un sistema di coordinate sferiche e l'asse delle  coincida con l'asse di simmetria del cilindro. Quest'ultimo giace nel semispazio delle
coincida con l'asse di simmetria del cilindro. Quest'ultimo giace nel semispazio delle  negative. La forza netta sulla carica è chiaramente diretta verticalmente. Un elemento di cono di area
negative. La forza netta sulla carica è chiaramente diretta verticalmente. Un elemento di cono di area 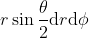 esercita sulla carica una forza la cui componente
esercita sulla carica una forza la cui componente  è:
è:

Dunque la forza totale si ottiene come:
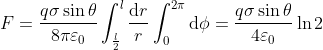
Chiaramente, la forza risulta massima per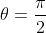 .
.
Dunque la forza totale si ottiene come:
Chiaramente, la forza risulta massima per
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: Carica sul cono
Scusa Luca sono l'ultimo venuto e può darsi che non abbia capito e abbia equivocato quello che hai scritto. L'angolo teta di apertura del cono dovrebbe essere quello fra il suo asse e l'apotema. Ora per teta=pigreco/2 mi pare che il tronco di cono si riduca ad una corona circolare centrata in q che darebbe luogo a forze orizzontali in cui quelle generate da elementi diametralmente opposti si eliderebbero. Cioè la forza sarebbe non massima ma complessivamente nulla ??? Forse il risultato è teta=pigreco/4???
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: Carica sul cono
Io ho inteso l'angolo di apertura come il doppio dell'angolo fra asse e apotema, chiaramente in caso contrario al mio  andrebbe sostituito
andrebbe sostituito 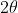 e l'angolo del massimo sarebbe
e l'angolo del massimo sarebbe 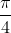 .
.
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: Carica sul cono
Luca il procedimento è giusto, però l'angolo di apertura è effettivamente ciò che ha detto Roncu, quindi dovresti sostituire  con
con 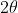 per ottenere il risultato corretto. Visto che l'errore è stato nella mia spiegazione poco chiara direi che la staffetta è tua, vai pure col 279
per ottenere il risultato corretto. Visto che l'errore è stato nella mia spiegazione poco chiara direi che la staffetta è tua, vai pure col 279 
Mi sembrava comunque giusto far notare a chiunque volesse provare che c'è un metodo per risolverlo senza integrali doppi, che se nessuno manda posterò io più avanti
Mi sembrava comunque giusto far notare a chiunque volesse provare che c'è un metodo per risolverlo senza integrali doppi, che se nessuno manda posterò io più avanti
Re: 278 - Carica sul cono
Tanto anche per esercitarmi a latex. Non avevo usato integrali doppi che non conosco ma integrali semplici. Detta 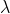 la variabile corrente sull'apotema, variabile fra l/2 e l, avevo diviso la superficie troncoconica in corone circolari infinitesime di raggio
la variabile corrente sull'apotema, variabile fra l/2 e l, avevo diviso la superficie troncoconica in corone circolari infinitesime di raggio 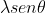 e spessore
e spessore 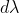 , fatte di punti equidistanti da q che esercitano su essa la forza infinitesima dF= kq.sigma.2pigreco.
, fatte di punti equidistanti da q che esercitano su essa la forza infinitesima dF= kq.sigma.2pigreco.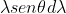 /
/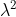 dove k è la costante di Coulomb. Pertanto il modulo della forza si ottiene integrando dF con
dove k è la costante di Coulomb. Pertanto il modulo della forza si ottiene integrando dF con 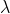 variabile fra l/2 e l. Viene il ln2 e il risultato sarebbe se non ho sbagliato i conti F=2pigreco kq sen
variabile fra l/2 e l. Viene il ln2 e il risultato sarebbe se non ho sbagliato i conti F=2pigreco kq sen sigma.ln2: Chiaramente F ha due componenti orizzontale e verticale. Le componenti orizzontali si elidono perchè due elementi diametralmente opposti di ogni coroncina danno luogo a forze orizzontali opposte. Le componenti verticali ottenute moltiplicando per cos
sigma.ln2: Chiaramente F ha due componenti orizzontale e verticale. Le componenti orizzontali si elidono perchè due elementi diametralmente opposti di ogni coroncina danno luogo a forze orizzontali opposte. Le componenti verticali ottenute moltiplicando per cos si sommano dando come risultato finale se non sbaglio F=2pigreco kq sen
si sommano dando come risultato finale se non sbaglio F=2pigreco kq sen sigma.ln2.cos
sigma.ln2.cos . Si vede facilmente che il massimo si ottiene per sen
. Si vede facilmente che il massimo si ottiene per sen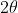 =1 cioè 2
=1 cioè 2 =pigreco/2 e quindi
=pigreco/2 e quindi 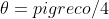 .
.
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 278 - Carica sul cono
Non riesco a modificare il mio messaggio originale, però @roncu ha ottenuto il risultato corretto evitando la doppia integrazione, praticamente saltando quella in 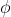 considerando direttamente le corone circolari. Pertanto, se @Rick è d'accordo, lascerei a lui il testimone.
considerando direttamente le corone circolari. Pertanto, se @Rick è d'accordo, lascerei a lui il testimone.
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 278 - Carica sul cono
@roncu perfetto, come dice @Luca Milanese la staffetta è tua 
Re: 278 - Carica sul cono
In altra situazione non so dove avrei potuto trovare un problema adeguato a voi così avanti rispetto a me  In questo caso però non avendo ricevuto risposte all'SNS 2021-1 vi prego di considerare quello il n.279 perchè non mi riesce di farci rientrare l'integrale suggerito - tanto non sarò solo a essere interessato al concorso di ammissione SNS!!
In questo caso però non avendo ricevuto risposte all'SNS 2021-1 vi prego di considerare quello il n.279 perchè non mi riesce di farci rientrare l'integrale suggerito - tanto non sarò solo a essere interessato al concorso di ammissione SNS!! 
