#piùcomplessisulforum!

Intanto carico la prima parte, tra poco dovrei postare anche la seconda:
Parte a) Notiamo innanzitutto che dopo l'n-esimo spegnimento, la particella si muoverà su una circonferenza di raggio
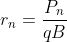
, dove
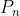
è il modulo della quantità di moto n-esima, che rimane costante tra spegnimento e accensione. Lo spostamento angolare in ogni intervallo
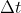
equivale all'angolo di cui ruota il vettore q.d.m. tra spegnimento e accensione, che è
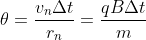
; quindi l'angolo di rotazione rimane costante, indipendentemente da

. L'impulso ricevuto a causa del campo sarà
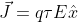
; visto che

, può essere considerato istantaneo.
La q.d.m.
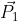
inizialmente sarà parallela ad
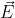
(all'istante dell'accensione,
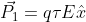
), poi ruoterà di un angolo

nell'intervallo
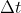
, quindi si sommerà con
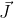
istantaneamente, diventanto
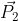
. A sua volta, questo vettore ruoterà di

in
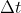
, poi si sommerà con
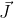
e così via.
Si può usare il piano complesso per facilitare i conti, ponendo l'asse x coincidente con quello reale, l'asse y con quello immaginario. Il processo appena illustrato corrisponde a porre

Si può dimostrare facilmente per induzione che
}))
per
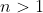
; segue che
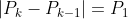
e che
}\equiv p_k)
per
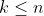
intero.
Perciò, ogni vettore
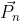
può essere scritto come somma di

vettori
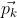
di modulo
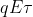
, con
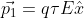
tali che l'angolo tra
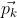
e
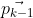
è sempre

.