Ebbene, Flaffo dovrebbe finire la tesina, ma scriviamo invece la soluzione per questo problema. Per evitare conti deliranti, che forse non tornerebbero, assumiamo che la lunghezza dei cilindri e del solenoide sia molto maggiore dei raggi dei rispettivi corpi, e che il campo magnetico prodotto dalla rotazione dei cilindri sia trascurabile.
Siano
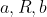
i raggi dei tre corpi rispettivamente, definiti in ordine crescente.
Il campo magnetico prodotto dal solenoide è quindi
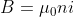
, mentre il flusso del campo magnetico nel primo e secondo solenoide vale rispettivamente:
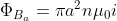
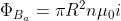
Per una delle leggi di elettromagnetismo, forse impropriamente attribuita a Maxwell, abbiamo:
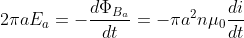
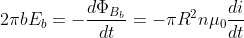
Il momento generato dal campo elettrico è quindi:


Per un'altra equazione importante sappiamo che:
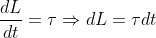
Dunque il momento angolare, in funzione del tempo, dei due cilindri rispetto al loro asse comune è:
}{dL}= \int_i^{i(t)}}{\tau dt})
Cioè, in funzione della corrente
}{dL_a} = \int_{i}^{i(t)}{- \frac{1}{2} a^2 Q n \mu_0 di } )
_a = \frac{1}{2} (i- i(t)) a^2 Q n \mu_0)
}{dL_b}= \int_i^{i(t)}{- \frac{1}{2} R^2 Q n \mu_0 di } )
_b = - \frac{1}{2} (i- i(t)) R^2 Q n \mu_0)
Nel tempo
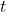
per cui
=0)
abbiamo allora:
)
Il campo magnetico alla fine è nullo, nelle approssimazioni fatte, quindi non vi è altro contributo al momento angolare.
Il momento angolare iniziale è invece quello contenuto nell'onda elettromagnetica e la sua densità è data da:
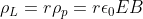
(Tanto sono perpendicolari nelle approssimazioni..). Per Gauss, il campo elettrico è solo presente nella zona
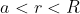
e vale:
= \frac{Q}{2 \pi l \epsilon_0} \frac{1}{r})
Dunque
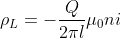
Perciò il momento angolare iniziale vale:
= \frac{1}{2} Q \mu_0 n i (a^2-R^2) )
Che è uguale a quello finale. QED
(Per gli ignoranti: quantum electrodynamics )
"No, no, you're not thinking; you're just being logical. "
