La ricerca ha trovato 128 risultati
- 19 ago 2021, 16:57
- Forum: Problemi teorici
- Argomento: 268-bagno elettrolitico
- Risposte: 4
- Visite : 2169
Re: 268-bagno elettrolitico
Si erano queste ultime densità che il testo intendeva conoscere. Vai con il 269! 


- 19 ago 2021, 10:27
- Forum: Problemi teorici
- Argomento: 268-bagno elettrolitico
- Risposte: 4
- Visite : 2169
Re: 268-bagno elettrolitico
E' tutto perfetto fino alla terza risposta dove, se capisco bene, dici che le densità di carica si ricavano da 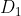 e
e 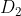 : Credo che la risposta al terzo quesito c) corrisponda proprio ad esplicitarle; ci sarebbe poi anche un "uniforme"che andrebbe spiegato...e puoi passare al 269!
: Credo che la risposta al terzo quesito c) corrisponda proprio ad esplicitarle; ci sarebbe poi anche un "uniforme"che andrebbe spiegato...e puoi passare al 269! 
- 17 ago 2021, 17:54
- Forum: Problemi teorici
- Argomento: 268-bagno elettrolitico
- Risposte: 4
- Visite : 2169
268-bagno elettrolitico
Un condensatore a facce piane e parallele quadrate di lato L distanti d è caricato al potenziale V e poi disconnesso dalla batteria. Successivamente viene inserito verticalmente in un bagno elettrolitico costituito da un liquido di costante dielettrica relativa \epsilon_r fino a che il liquido riemp...
- 15 ago 2021, 11:16
- Forum: Problemi teorici
- Argomento: 267. Infinitupolo
- Risposte: 15
- Visite : 5778
Re: 267. Infinitupolo
In verità per maggiore sicurezza mi ero fatto questa obiezione: siccome x* non è proprio (x/2L) ma il max intero in esso contenutox* non annulla proprio (x/2L) per cui il primo termine è qualcosa più di 1, il secondo qualcosa più di 2 ecc. per cui in realtà la parentesi contiene numeri compresi fra ...
- 14 ago 2021, 18:00
- Forum: Problemi teorici
- Argomento: 267. Infinitupolo
- Risposte: 15
- Visite : 5778
Re: 267. Infinitupolo
L'idea era quella di poter sfruttare quello che mi pare era anche il tuo suggerimento e cioè che \sum_1^\infty \frac {1}{n^4} = \pi^4/90 Dovevo fare in modo che la parentesi di [(x/2L)+n]^4 si comportasse come l'n di prima cioè andasse da 1 a \infty . Ed infatti quando n=-x*+1, l'intera parentesi va...
- 13 ago 2021, 18:05
- Forum: Problemi teorici
- Argomento: 267. Infinitupolo
- Risposte: 15
- Visite : 5778
Re: 267. Infinitupolo
Fermi restando i due punti A)(dipolo) e B)(quadrupolo) riprendo il punto C) relativo all'infinitopolo (quadrupolo + un numero infinito di quadrupoli ciascuno a distanza 2L dal precedente). Risulterà allora E_\infty = \frac{12 e L^2}{4\pi \epsilon_0}. [\frac{1}{x^4} + \frac{1}{(x+2L)^4}+....]= \frac{...
- 13 ago 2021, 11:44
- Forum: Problemi teorici
- Argomento: 267. Infinitupolo
- Risposte: 15
- Visite : 5778
Re: 267. Infinitupolo
Si grazie infatti manca il coefficiente che è lo stesso di 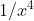 e cioè
e cioè /(4\pi\epsilon_0)) . Appena ho tempo lo rimetterò per bene. Scusate.
. Appena ho tempo lo rimetterò per bene. Scusate. 
- 12 ago 2021, 17:04
- Forum: Problemi teorici
- Argomento: 267. Infinitupolo
- Risposte: 15
- Visite : 5778
Re: 267. Infinitupolo
Allora abbiamo da parte dell'infinitopolo un campo E dato dall'espressione E=\frac{12 e L^2}{4\pi.\epsilon_0.x^4}+\sum_n\frac{1}{(x+2Ln)^4} . Ora gli addendi della somma, evidenziando a denominatore (2L)^4 , possono scriversi come \frac{1}{(2L)^4[(x/2L)+n]^4} . Il trucco di cui ti parlavo sarebbe qu...
- 11 ago 2021, 11:17
- Forum: Problemi teorici
- Argomento: 267. Infinitupolo
- Risposte: 15
- Visite : 5778
Re: 267. Infinitupolo
Temo di non capire. Pensi a qualcosa di analogo al cambio degli estremi di integrazione negli integrali? Comunque grazie del valore della serie che avevo visto anch'io come applicazione del teorema di Parseval (così avevo letto) :roll: :roll: Propendo per un altro trucco che domani posterò (oggi non...
- 10 ago 2021, 18:00
- Forum: Problemi teorici
- Argomento: 267. Infinitupolo
- Risposte: 15
- Visite : 5778
Re: 267. Infinitupolo
Figurati io con le serie...Allora comunque credo che sia corretta l'impostazione con la serie del mio post precedente. Allora ho considerato il denominatore della sommatoria sviluppandolo. Lo faccio senza scrivere la linea di frazione tanto ci intendiamo. Abbiamo (x+2Ln)^4= (x+2Ln)^2.(x+2Ln)^2= (x^2...
