Inductance Puzzle
-
Physicsguy51
- Messaggi: 62
- Iscritto il: 13 nov 2022, 5:06
Inductance Puzzle
We have a small ring made of thin wire having radius  and its inductance is
and its inductance is  . Find the inductance of a ring having
. Find the inductance of a ring having  -times the dimensions as this ring. If in the plane of the ring, we place another superconducting ring of half the geometric dimensions so that the planes of the rings and their centers coincide, then the inductance of the ring with radius
-times the dimensions as this ring. If in the plane of the ring, we place another superconducting ring of half the geometric dimensions so that the planes of the rings and their centers coincide, then the inductance of the ring with radius  comes out to be
comes out to be 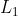 . What will the inductance
. What will the inductance 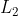 of the ring with radius
of the ring with radius  be when it is placed inside a superconducting ring with twice the geometric dimensions? The planes and centers of the rings also coincide in this case.
be when it is placed inside a superconducting ring with twice the geometric dimensions? The planes and centers of the rings also coincide in this case.
-
Tarapìa Tapioco
- Messaggi: 146
- Iscritto il: 30 lug 2023, 15:28
Re: Inductance Puzzle
Striking problem. Where did you get that?
-
Physicsguy51
- Messaggi: 62
- Iscritto il: 13 nov 2022, 5:06
Re: Inductance Puzzle
It is a problem from Russian olympiad. Give it a try, it is a nice puzzle and has a nice solution.
-
Tarapìa Tapioco
- Messaggi: 146
- Iscritto il: 30 lug 2023, 15:28
Re: Inductance Puzzle
Sure, during these days I will try to solve this problem and also the other you proposed.
-
Physicsguy51
- Messaggi: 62
- Iscritto il: 13 nov 2022, 5:06
Re: Inductance Puzzle
Ok, thank you!
I'll propose some other challenging problems from Rudolf Ortvay since they do not have official solutions anywhere.
I'll propose some other challenging problems from Rudolf Ortvay since they do not have official solutions anywhere.
-
Tarapìa Tapioco
- Messaggi: 146
- Iscritto il: 30 lug 2023, 15:28
Re: Inductance Puzzle
Physicsguy51 ha scritto: ↑30 ago 2023, 5:07 We have a small ring made of thin wire having radiusand its inductance is
. Find the inductance of a ring having
-times the dimensions as this ring. If in the plane of the ring, we place another superconducting ring of half the geometric dimensions so that the planes of the rings and their centers coincide, then the inductance of the ring with radius
comes out to be
. What will the inductance
of the ring with radius
be when it is placed inside a superconducting ring with twice the geometric dimensions? The planes and centers of the rings also coincide in this case.
This problem has a medium-high difficulty coefficient, but it's striking, especially because of the challenging entanglements making up the puzzle.
Let us recall the formula for the inductance of a ring of radius
Now, suppose having another ring that has
So, the inductance of the scaled-up ring is
In a more general way, it can therefore be written:
The placing of superconductors inside (smaller size) or outside (larger size) of an original ring, so that their planes and centers coincide, is the case involving concentric and coplanar rings, which make up a puzzle through which the starting ring changes its self-inductance depending on the loop in contact with it. The interest of the problem is to calculate the inductance
The magnetic flux
1) the flux
2) The flux
So:
1)
2)
Hence it follows that
In conclusion, regarding 1), the flux
The net internal flux
Since it has been proved that the inductance of a ring with dimensions
Since the coil of radius
By equating the two expressions for
Substituting
By means of the mutual induction approach, it is possible to obtain, for
In analogy to what we saw earlier with expression (1), we have that:
As discussed previously, the magnetic flux
Equalizing the two expressions for
Substituting
Picking up 2), the flux
The net external flux
Since it has been shown that the inductance of a ring having dimensions
Since the loop of radius
Equalizing the two expressions for
Substituting
For
Therefore, the external flux
As seen above with the expression
As discussed before, the flux
Equalizing the two expressions for
Substituting
Comparing the two expressions for
Ultima modifica di Tarapìa Tapioco il 19 ott 2023, 12:06, modificato 5 volte in totale.
-
Tarapìa Tapioco
- Messaggi: 146
- Iscritto il: 30 lug 2023, 15:28
Re: Inductance Puzzle
Si ricordi la formula che definisce l'induttanza di un anello avente raggioPhysicsguy51 ha scritto: ↑30 ago 2023, 5:07 We have a small ring made of thin wire having radiusand its inductance is
. Find the inductance of a ring having
-times the dimensions as this ring. If in the plane of the ring, we place another superconducting ring of half the geometric dimensions so that the planes of the rings and their centers coincide, then the inductance of the ring with radius
comes out to be
. What will the inductance
of the ring with radius
be when it is placed inside a superconducting ring with twice the geometric dimensions? The planes and centers of the rings also coincide in this case.
Si noti che l'induttanza
Ora, si supponga di considerare un altro anello che abbia
Quindi, l'induttanza di un anello ridimensionato è
Più in generale, si può dunque scrivere:
L'inserimento di superconduttori all'interno (di minori dimensioni) o all'esterno (di maggiori dimensioni) di un anello originario in modo che i loro piani e centri coincidano è il caso di anelli concentrici e complanari, i quali compongono un incastro grazie al quale l'anello di partenza modifica la propria auto-induttanza a seconda della spira a contatto con esso. L'interesse del problema è calcolare l'induttanza
Il flusso
1) il flusso
2) il flusso
Dunque:
1)
2)
Da ciò si evince che
In conclusione, per quanto concerne 1), il flusso
Il flusso netto interno
Poiché si è dimostrato che l'induttanza di un anello avente dimensioni
Poiché la spira di raggio
Eguagliando le due espressioni per
Sostituendo la
Tramite l'applicazione della mutua induzione, è possibile pervenire, per
Analogamente a quanto visto precedentemente con l'espressione
Come discusso prima, il flusso
Uguagliando le due espressioni per
Sostituendo la
Riprendendo 2), il flusso
Il flusso netto esterno
Poiché si è dimostrato che l'induttanza di un anello avente dimensioni
Poiché la spira di raggio
Eguagliando le due espressioni per
Sostituendo la
Anche per
Pertanto, il flusso esterno
Analogamente a quanto visto precedentemente con l'espressione
Come discusso prima, il flusso
Uguagliando le sue espressioni per
Sostituendo la
Confrontando le due espressioni per
